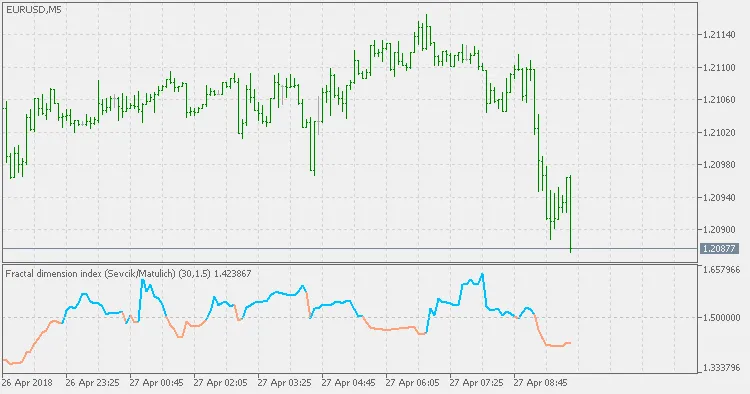
フラクタル次元指数(FDI)についての説明です。
マンデルブロは、フラクタル次元指数を「どれだけ複雑で不規則であるか」を測る方法として説明しています。このFDIは、株式市場のインジケーターとして利用可能です。
市場の価格は「トレンドしている」または「レンジしている」と考えることができます。強い上昇トレンドの際、価格は急激に動き、一時的に一次元の直線に近づくことがあります。しかし、価格がよりギザギザのフラクタルパターンで動くべきだと考える場合、ほぼ直線的な動きは、ある程度の精度で予測できるポイントで終わると仮定します。
トレンドが続いた後、価格はしばらくの間レンジで取引され、次のトレンドに向かうことがよくあります。価格が長方形のパターンで、同じポイントをジグザグに行き来する様子を想像してください。平面はフラクタルでもなければ直線でもないため、価格がレンジをブレイクし、再びフラクタルのように動くことが期待されます。
このように、FDIはチャート上のラインに数値を割り当てる方法です。この数値は1.0から2.0の間にあり、価格が一次元の直線に近づくほどFDIは1.0に近づき、二次元の平面に近づくほどFDIは2.0に近づきます。
このバージョンは、FDIの原作者カーロス・セブチックによって説明された通りに作成されていますが、一つ修正があります。セブチックが公表した公式は逆になっていました。このエラーはアレックス・マトゥリッチによって修正され、ここで使用されているのは正しい計算です。