Fraktale Dimension: Der Fractal Dimension Index (FDI) für MetaTrader 5

Mandelbrot beschreibt den Fractal Dimension Index als ein Maß dafür, „wie verworren und unregelmäßig“ etwas ist. Der FDI kann als Indikator für den Aktienmarkt verwendet werden.

Wir können die Preise in einem Markt als „trendend“ oder „seitwärts“ betrachten. Während eines starken Aufwärtstrends bewegen sich die Preise oft in einer scharfen Linie, die fast eindimensional wirkt. Wenn wir jedoch davon ausgehen, dass die Preise sich in einem unregelmäßigen, fraktalen Muster bewegen sollten, können wir vorhersagen, dass diese fast gerade Bewegung irgendwann enden wird, was uns eine gewisse Genauigkeit für einen profitablen Trade bietet.

Nach einem Trend handeln die Preise häufig eine Zeit lang in einer Range, bevor sie sich auf die nächste Trendbewegung zubewegen. Man kann sich das wie ein Rechteck vorstellen, in dem die Preise hin und her schwanken und dabei die gleichen Punkte in einem zweidimensionalen Muster durchlaufen. Eine Ebene ist ebenso wenig ein Fraktal wie eine gerade Linie, weshalb wir erwarten können, dass die Preise aus der Range ausbrechen und wieder fraktalartig agieren.

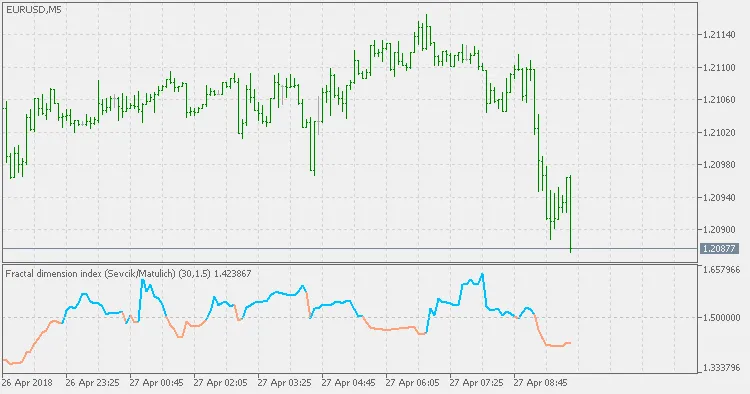
Der FDI ist somit ein Verfahren, das einer Linie auf deinem Chart eine Zahl zuweist. Diese Zahl liegt zwischen 1,0 und 2,0. Je näher sich die Preise an einer eindimensionalen geraden Linie bewegen, desto näher kommt der FDI an 1,0 heran. Je mehr die Preise einem zweidimensionalen Muster ähneln, desto näher bewegt sich der FDI an 2,0.