정의:
피어슨 상관계수는 두 변수의 공분산을 두 변수의 표준편차의 곱으로 나눈 값입니다. 이러한 정의는 '곱의 모멘트'를 포함하는데, 이는 평균을 조정한 확률 변수의 곱의 평균(원점에 대한 첫 번째 모멘트)을 의미합니다. 그래서 곱-모멘트라는 수식어가 붙습니다. 더 많은 정보는 여기에서 확인하실 수 있습니다: https://en.wikipedia.org/wiki/Pearson_correlation_coefficient
이 버전:
이 버전은 현재 차트 심볼에서의 계수를 계산할 수 있을 뿐만 아니라 두 개의 심볼 간의 상관계수도 계산할 수 있게 해줍니다.
- "두 번째 심볼" 파라미터에 빈 값을 설정하면 현재 차트 심볼이 사용됩니다. 이 경우 "지연" 파라미터는 반드시 0보다 큰 값으로 설정해야 하며, 그렇지 않으면 결과는 항상 0이 됩니다.
- "두 번째 심볼" 파라미터에 현재 심볼 차트와 다른 유효한 심볼을 설정하면 해당 심볼이 사용됩니다. 이 경우 "지연" 파라미터는 0으로 설정해야 하며(상응하는 바를 계산하기 위해), 지연을 추가할 수도 있지만, 이 경우 두 번째 심볼 데이터가 실제로 지연된다는 점을 유의해야 합니다.
사용법:
상관 지표와 마찬가지로, 예상되는 상관관계에 변동이 있을 때 이를 신호로 활용하여 적절한 조치를 취할 수 있습니다 (상관 거래 스타일에서).
예시:
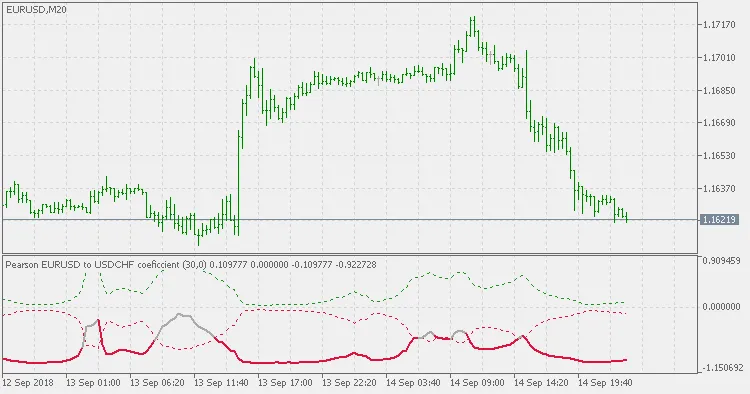
현재 심볼에서 1 바 지연:
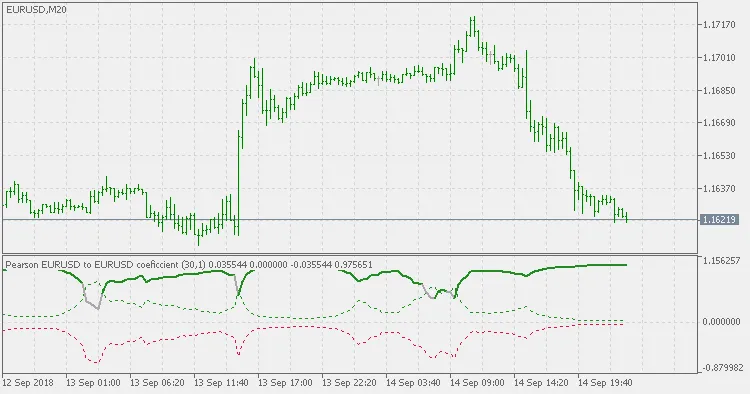
외국 심볼에서 0 바 지연: