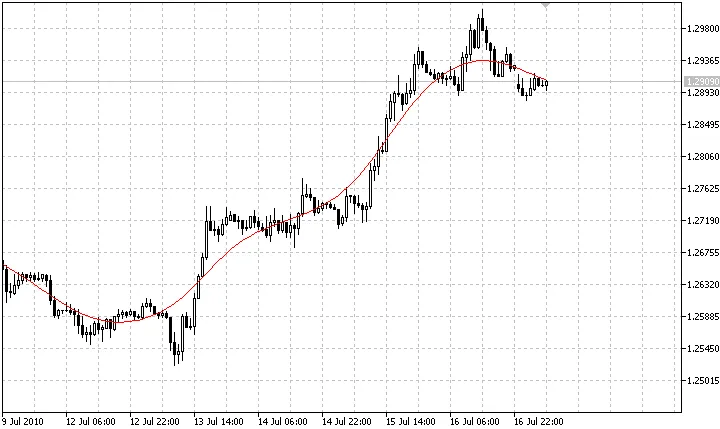
होड्रिक-प्रेस्कॉट फ़िल्टर का उपयोग मैक्रोइकोनॉमिक्स में किया जाता है, खासकर वास्तविक व्यापार चक्र सिद्धांत में, ताकि समय श्रृंखला के चक्रीय घटक को कच्चे डेटा से अलग किया जा सके। इसकी विशेषता यह है कि इसमें कोई लैग नहीं होता है। लेकिन ऐसे शून्य लैग फ़िल्टर का एक सामान्य नुकसान यह है कि हाल के मानों को फिर से गणना की जाती है.
मैंने इस फ़िल्टर को विभिन्न उद्देश्यों के लिए लागू करने की कोशिश की है: जैसे मूल्य चैनल के लिए, इसे प्रवृत्ति परिवर्तन संकेतक के रूप में उपयोग करने के लिए, आदि। लेकिन मैंने पाया कि इसकी तुलना में EMA, LWMA या AMA के साथ कोई महत्वपूर्ण लाभ नहीं है।
इसके अलावा, मैंने पाया कि इस फ़िल्टर द्वारा समतलित कीमतों के मान प्रिंसिपल कंपोनेंट एनालिसिस (PCA) के मुख्य घटक के करीब हैं। ऐसा प्रतीत होता है कि होड्रिक-प्रेस्कॉट फ़िल्टर और PCA के बीच एक गणितीय संबंध है। यह उपयोगी हो सकता है, इसलिए मैं इसे यहाँ प्रकाशित कर रहा हूँ। मैं इसका उपयोग नहीं करता, लेकिन अगर आप इसके संभावित अनुप्रयोगों का सुझाव दें तो यह बहुत अच्छा होगा।