आजकल, वित्तीय समय श्रृंखलाओं का सबसे लोकप्रिय प्रतिनिधि फ्रैक्टल टाइम फंक्शन है। इन श्रृंखलाओं की फ्रैक्टल संरचना सर्वविदित है।
मेंडलब्रॉट के अनुसार, एक प्रसिद्ध बाजार कहावत का यह पुनः शब्दांकन है कि शेयरों और मुद्राओं की गति समय स्केल और कीमत से स्वतंत्र है। एक पर्यवेक्षक चार्ट के दृश्य को देखकर यह नहीं बता सकता कि जानकारी साप्ताहिक, दैनिक या घंटे के बदलावों से संबंधित है।
फ्रैक्टल डायमेंशन निर्धारित करने के लिए आमतौर पर हर्स्ट का गुणांक (Hurst's Exponent) निकाला जाता है। हालाँकि, इस गुणांक की सटीक गणना के लिए बड़ी मात्रा में डेटा की आवश्यकता होती है (~ 103), जो ट्रेडिंग के ट्रेंड की अवधि की तुलना में बहुत अधिक है।
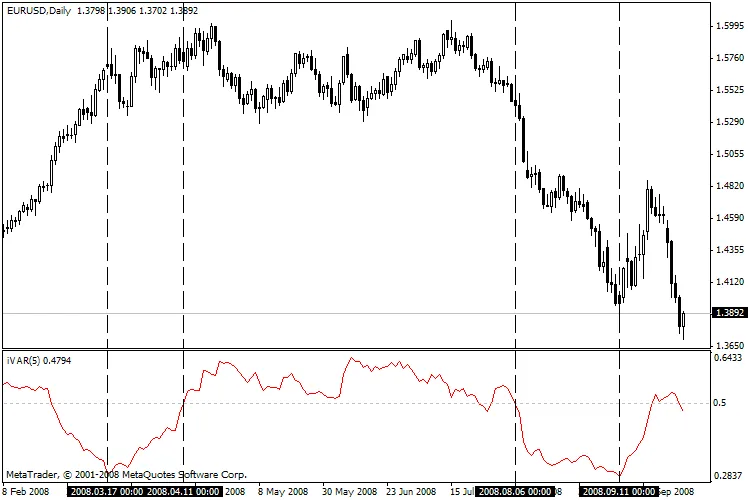
लेखक वेरिएशन इंडेक्स (m) का उपयोग करते हैं, जो सामान्य फ्रैक्टल डायमेंशन से निकटता से संबंधित है। हर्स्ट के गुणांक के विपरीत, इंडेक्स की गणना के लिए आवश्यक जानकारी की मात्रा 2 गुना कम है। यह इसे मूल्य श्रृंखला की गतिशीलता के निर्धारण के लिए एक स्थानीय विशेषता के रूप में उपयोग करने की अनुमति देता है। यदि m < 0.5 है, तो इसे एक ट्रेंड के रूप में व्याख्यायित किया जा सकता है, और यदि m > 0.5 है तो इसे फ्लैट के रूप में देखा जा सकता है।
यह संकेतक पिछले अंतराल पर वेरिएशन इंडेक्स की गणना करता है जो 2n लंबा होता है। 'n' पैरामीटर को उपयोगकर्ता द्वारा निर्दिष्ट किया जाता है।
संकेतक के उपयोग के सामान्य नियम इस प्रकार हैं:
- यदि संकेतक का मान 0.5 से कम है, तो यह बाजार की ट्रेंड स्थिति को दर्शाता है।
- अत्यधिक कम मान अक्सर वर्तमान ट्रेंड के अंत (सुधार) का पूर्वानुमान करता है।
- यदि संकेतक का मान 0.5 से अधिक है, तो यह बाजार की फ्लैट स्थिति को दर्शाता है।
- अत्यधिक उच्च मान अक्सर महत्वपूर्ण ट्रेंड की शुरुआत का संकेत देता है।
- यदि संकेतक का मान 0.5 के करीब है, तो यह बाजार की अनिर्धारित स्थिति को दर्शाता है।
साहित्य:
1. M.M. Dubovikov और अन्य। डायमेंशन ऑफ द मिनिमल कवर एंड लोकल एनालिसिस ऑफ फ्रैक्टल टाइम सीरीज, 2004।
2. Edgar E. Peters, फ्रैक्टल मार्केट एनालिसिस। अप्लाईंग कैओस थ्योरी टू इन्वेस्टमेंट एंड इकोनॉमिक्स, John Wiley & Sons, 2003।
