वास्तविक लेखक:
वेरिएशन इंडेक्स यह दर्शाता है कि किसी समय श्रृंखला में प्रवृत्ति या समतल गति प्रचलित है या नहीं, या यह बेतरतीब व्यवहार है।
आजकल, वित्तीय समय श्रृंखलाएँ फ्रैक्टल समय कार्यों के सबसे लोकप्रिय प्रतिनिधि हैं। इन श्रृंखलाओं की फ्रैक्टल संरचना अच्छी तरह से ज्ञात है और मंडेलब्रॉट के अनुसार यह "एक व्यावहारिक बाजार लोकाचार का सैद्धांतिक पुनःफॉर्मुलेशन है - अर्थात्, जब एक बाजार चार्ट को बढ़ाया या घटाया जाता है, तो एक स्टॉक या मुद्रा की गतिविधियाँ सभी एक जैसी दिखती हैं" [1]।
आम तौर पर, फ्रैक्टल आयाम निर्धारित करने के लिए हर्स्ट का गुणांक (Hurst's exponent) गणना की जाती है [2]। हालांकि, इस गुणांक की विश्वसनीय गणना के लिए बहुत अधिक डेटा (~ 10^3) की आवश्यकता होती है, जो व्यापार प्रवृत्तियों की अवधि की तुलना में बहुत अधिक है।
लेखकों ने फ्रैक्टल विशेषताओं को जोड़ते हुए वेरिएशन इंडेक्स (m) प्रस्तुत किया है जो सामान्य फ्रैक्टल आयाम से निकटता से संबंधित है। हर्स्ट के गुणांक के विपरीत, इंडेक्स निर्धारण के लिए आवश्यक जानकारी की मात्रा 2 गुना कम होती है। इससे इसे मूल्य श्रृंखला की गतिशीलता के निर्धारण के लिए एक स्थानीय विशेषता के रूप में उपयोग करना संभव हो जाता है। यदि m < 0.5 है, तो इसे प्रवृत्ति के रूप में व्याख्यायित किया जा सकता है और यदि m > 0.5 है, तो इसे समतल के रूप में व्याख्यायित किया जा सकता है।
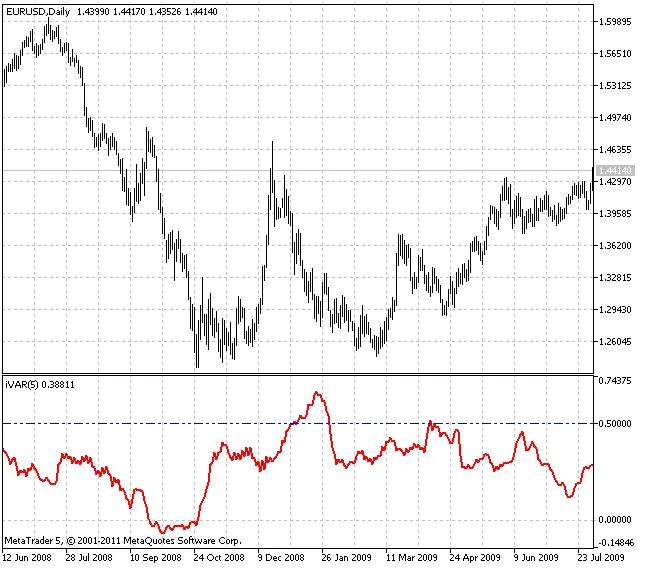
प्रस्तावित संकेतक पिछले अंतराल पर वेरिएशन इंडेक्स की गणना करता है जो 2^n लंबा होता है। "n" पैरामीटर उपयोगकर्ता द्वारा निर्दिष्ट किया जाता है।
इंडिकेटर के आवेदन के सामान्य नियम निम्नलिखित हैं:
- यदि संकेतक का मान 0.5 से कम है, तो इसका अर्थ है कि मार्केट की प्रवृत्ति की स्थिति है।
- अत्यधिक निम्न मान अक्सर वर्तमान प्रवृत्ति के अंत (सुधार) से पहले होता है।
- यदि संकेतक का मान 0.5 से अधिक है, तो इसका अर्थ है कि मार्केट की समतल स्थिति है।
- अत्यधिक उच्च मान अक्सर महत्वपूर्ण प्रवृत्तियों की शुरुआत से पहले होता है।
- यदि संकेतक का मान 0.5 के निकट है, तो इसका अर्थ है कि मार्केट की स्थिति अस्पष्ट है।
यह संकेतक पहली बार MQL4 में लागू किया गया था और CodeBase पर mql4.com पर 06.10.2008 को प्रकाशित हुआ था।
संदर्भ
- M.M. Dubovikov et al, Dimension of the Minimal Cover and Local Analysis of Fractal Time Series, 2004.
- Edgar E. Peters, Fractal Market Analysis. Applying Chaos Theory to Investment and Economics, John Wiley & Sons, 2003.
