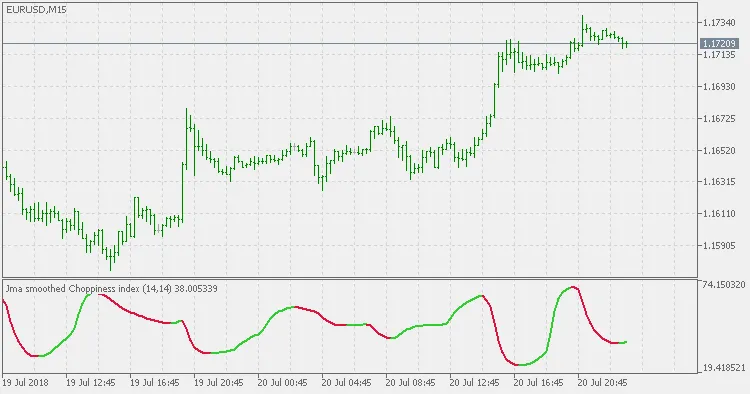
चॉपिनेस इंडेक्स: एक और तरीका जो फ्रैक्टल डाइमेंशन की गणना करता है।
चॉपिनेस क्या है?
चॉपिनेस एक आधुनिक संकेतक है जो अराजकता सिद्धांत और फ्रैक्टल ज्यामिति के विचारों पर आधारित है। फ्रैक्टल ज्यामिति के विषय में सबसे अधिक रुचि रखने वाले व्यक्ति बेनोइट मंडेलब्रॉट थे। उन्होंने दिखाया कि फ्रैक्टल्स गणित और प्रकृति में कई अलग-अलग स्थानों पर कैसे पाए जा सकते हैं। ये बादलों के आकार, लहरों, पत्तियों, अंगुलियों के निशान और सूरजमुखी में छिपे होते हैं, और उनके विचारों ने गणित और प्रकृति के बीच एक रोमांचक संबंध प्रस्तुत किया। कंप्यूटर ग्राफिक्स का उपयोग करते हुए, मंडेलब्रॉट ने IBM की मदद से दिखाया कि कैसे फ्रैक्टल ज्यामिति को कंप्यूटर ग्राफिक्स के माध्यम से व्यक्त किया जा सकता है।
जबकि हम में से अधिकांश यह सोचते हैं कि केवल पूरे संख्या वाले डाइमेंशन होते हैं, जैसे 1D, 2D, और 3D, फ्रैक्टल ज्यामिति में पूरे संख्या वाले डाइमेंशन के बीच भिन्नात्मक डाइमेंशन होते हैं। इसलिए एक 1D रेखा और 2D सतह के बीच कई फ्रैक्टल डाइमेंशन होते हैं। फ्रैक्टल्स मूल रूप से किसी सिस्टम की डाइमेंशनलिटी का मापन हैं; वे भिन्नात्मक डाइमेंशन के आधार पर विभिन्न छवियों को व्यक्त कर सकते हैं।
ऑस्ट्रेलिया के एक व्यापारी, ई. डब्ल्यू. ड्रेइस ने यह अनूठा विचार प्रस्तुत किया कि फ्रैक्टल ज्यामिति का उपयोग एक सुरक्षा में मूल्य आंदोलन को मापने के लिए किया जा सकता है। उन्होंने बुद्धिमानी से मूल्य आंदोलन चार्ट को एक "डाइमेंशन" सौंपा। एक चार्ट जो ट्रेंड कर रहा था और रेखीय था, उसे पूरे डाइमेंशन 1 का मूल्य दिया जा सकता था, जबकि एक चार्ट जो पूरी तरह से चॉपिन और न ट्रेंड कर रहा था, उसे डाइमेंशन 2 का माना जा सकता था। इन दोनों मूल्यों के बीच कहीं भिन्नात्मक अवस्थाएँ और विभिन्न चॉपिनेस के डिग्री का प्रतिनिधित्व किया जाता है।
चॉपिनेस इंडेक्स संकेतक की तुलना में, यह संस्करण JMA का उपयोग कर रहा है जिसे स्मूथिंग के लिए प्रयोग किया गया है (चॉपिनेस इंडेक्स की ढलान दिशा परिवर्तन को पहचानना आसान बनाने के लिए) और मूल्यों को कम अस्थिर बनाने के लिए।