क्वांटाइल बैंड्स एक ऐसा इंडिकेटर है जो विभिन्न क्वांटाइल्स का उपयोग करके मूल्यांकन करता है।
आंकड़ों और संभाव्यता के सिद्धांत में, क्वांटाइल्स ऐसे कट प्वाइंट होते हैं जो एक संभाव्यता वितरण के रेंज को समान संभावनाओं के साथ लगातार अंतरालों में विभाजित करते हैं, या एक नमूने में अवलोकनों को इसी तरह विभाजित करते हैं। समूह बनाने के लिए क्वांटाइल्स की संख्या में एक कम होता है। उदाहरण के लिए, क्वारटाइल्स तीन कट प्वाइंट होते हैं जो एक डेटा सेट को चार समान आकार के समूहों में बांटते हैं। सामान्य क्वांटाइल्स के विशेष नाम होते हैं: जैसे कि क्वारटाइल, डेसाइल (जो 10 समूह बनाते हैं)। बनाए गए समूहों को आधे, तिहाई, चौथाई आदि कहा जाता है, हालांकि कभी-कभी समूहों के लिए क्वांटाइल के नाम का उपयोग किया जाता है।
q-क्वांटाइल्स वे मान हैं जो एक सीमित सेट के मानों को q लगभग समान आकार के उप-सेट्स में विभाजित करते हैं। इनमें q − 1 q-क्वांटाइल्स होते हैं, जिसमें हर पूर्णांक k के लिए एक होता है, जो 0 < k < q को संतुष्ट करता है। कुछ मामलों में, क्वांटाइल का मान अद्वितीय नहीं हो सकता है, जैसे कि मीडियन (2-क्वांटाइल) के लिए। क्वांटाइल्स को निरंतर वितरणों पर भी लागू किया जा सकता है, जो निरंतर चर के लिए रैंक सांख्यिकी को सामान्य बनाने का एक तरीका प्रदान करता है। जब एक संचयी वितरण कार्य ज्ञात होता है, तो q-क्वांटाइल्स क्वांटाइल फ़ंक्शन का उपयोग करते हैं।
लेकिन यहाँ एक विचलन और "सामान्यीकृत" है।
क्वांटाइल बैंड्स के सभी संस्करण तीन कीमतों का उपयोग करते हैं। लेकिन यह संस्करण केवल एक कीमत का उपयोग करता है, और उच्च और निम्न के बीच (महत्वपूर्ण) अंतर बनाने के लिए, आप उच्च और निम्न मान खोजने के लिए अवधि चुन सकते हैं। लेकिन इसके बिना भी (जब उच्च/निम्न अवधि <=1 पर सेट होती है) बैंड्स की गणना ठीक से काम करती है, और अधिकांश मामलों में उच्च/निम्न अवधि को सक्रिय करने की आवश्यकता नहीं होती है।
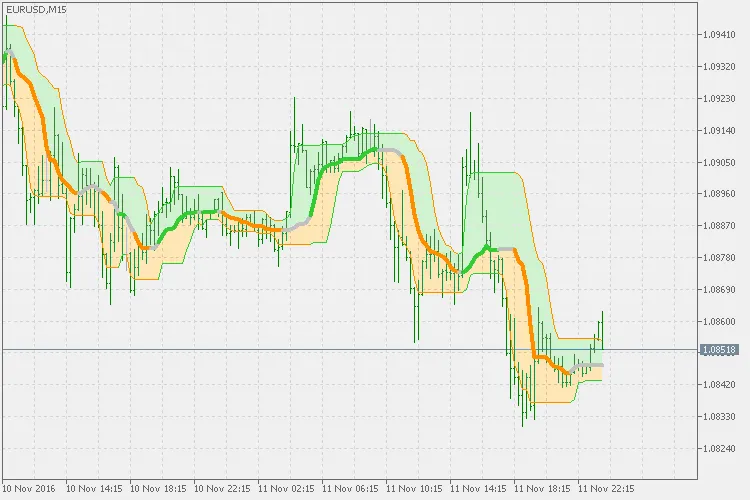
"सामान्यीकृत" नाम के पीछे का कारण:
यह इंडिकेटर किसी अन्य इंडिकेटर पर भी लागू किया जा सकता है। इसलिए, इसे जरूरी नहीं है कि इसे केवल कीमतों पर लागू किया जाए। और इसका कुछ उपयोग (जैसे कि क्वांटाइल बैंड्स को RSI और स्टोकास्टिक पर लागू करना) काफी दिलचस्प परिणाम दे सकता है।
