Smoothed ADX: Der Indikator für präzisere Handelsentscheidungen

Der Smoothed ADX-Indikator wurde auf Anfrage eines Forumsteilnehmers erstellt und ist nicht allzu kompliziert. Allerdings fand ich keine Beschreibung des Algorithmus für den gleitenden ADX, weshalb ich hier nur den bereitgestellten Code teile:

Inputs:
Length(14), ADXTrend(25), alpha1(0.25), alpha2(0.33);

Variablen:
DMIPlus(0), DMIMinus(0), DMI(0), ADX(0),
DIPlusLead(0), DIMinusLead(0), DIPlusFinal(0), DIMinusFinal(0),
ADXLead(0), ADXFinal(0);

{Jetzt rufen wir die eingebauten ADX-Funktionen auf, sodass wir sie nicht selbst berechnen müssen}

Value1 = DirMovement(H, L, C, Length, DMIPlus, DMIMinus, ADX);

{Dieser Teil ist die eigentliche Glättung des ursprünglichen ADX-Indikators. DI+, DI- und ADX-Linien werden geglättet}

DIPlusLead = 2*DMIPlus + (alpha1 - 2) * DMIPlus[1] + (1 - alpha1) * DIPlusLead[1];
DIPlusFinal = alpha2*DIPlusLead + (1 - alpha2) * DIPlusFinal[1];

DIMinusLead = 2*DMIMinus + (alpha1 - 2) * DMIMinus[1] + (1 - alpha1) * DIMinusLead[1];
DIMinusFinal = alpha2*DIMinusLead + (1 - alpha2) * DIMinusFinal[1];

ADXLead = 2*ADX + (alpha1 - 2) * ADX[1] + (1 - alpha1) * ADXLead[1];
ADXFinal = alpha2*ADXLead + (1 - alpha2) * ADXFinal[1];

{Jetzt werden sie im Chart dargestellt}

Plot1(DIPlusFinal, "DMI+");
Plot2(DIMinusFinal, "DMI-");
Plot3(ADXFinal, "ADX");

Wenn man nicht versucht, den tieferen Sinn hinter dem ursprünglichen Text des geglätteten ADX zu verstehen, kann man die Glättung in zwei Phasen unterteilen. Angenommen, wir haben eine numerische Sequenz P und müssen diese mit minimaler Verzögerung glätten. Dafür bauen wir in der ersten Phase die Funktion V(P) der P-Sequenz-Oszillation aus der folgenden Formel auf:

V0 = (8*P0 - 7*P1 + 3*V1) / 4,
wobei:

P0 der aktuelle Wert der Sequenz (ein Preis oder ein Indikator) ist;
P1 der vorhergehende Wert der Sequenz ist;
V1 der vorhergehende Wert der Oszillation ist;
V0 der aktuelle Wert der Oszillation ist.

Oder anders ausgedrückt:
V0 = (Vol(P) + 3*V1) / 4,
wobei:
Vol(P) = 8*P0 - 7*P1 - Ehlers' Burst (ein Begriff, den ich selbst erfunden habe).

In der zweiten Phase wenden wir die einfache gewichtete Glättung an:
W0 = (1*V0 + 2*W1) / (2 + 1),
wobei:

W0 der aktuelle geglättete Wert der Sequenz P ist;
V0 der aktuelle Wert der P-Sequenz-Oszillation ist;
W1 der vorhergehende geglättete Wert ist.

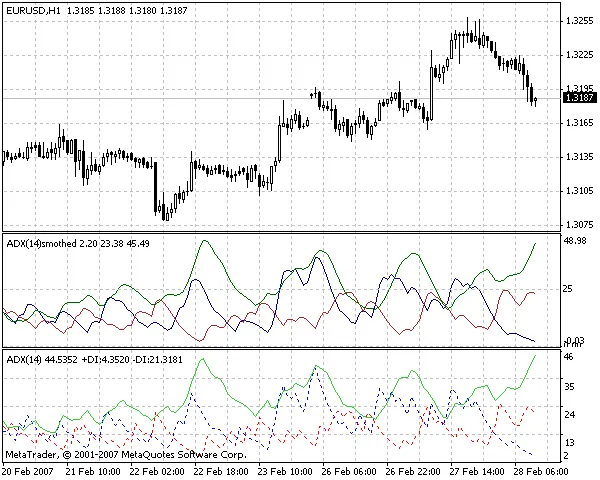
Beim Smoothed ADX wird dieser Glättungsalgorithmus auf alle drei Puffer des Standard-Indikators ADX angewendet. Deshalb wird der erhaltene Indikator als Smoothed ADX bezeichnet. Wenn wir den Indikator RSI glätten würden, würden wir ihn Smoothed RSI nennen usw. Die folgende Abbildung zeigt, dass der Smoothed ADX tatsächlich weniger „zappelig“ ist als der ursprüngliche, standardmäßige ADX (Average Directional Movement Index).

Smoothed ADX: Der Indikator für präzisere Handelsentscheidungen

Verwandte Beiträge