Ein mehrharmonisches (oder mehrstimmiges) trigonometrisches Modell einer Preisserie x[i], für i=1..n, wird wie folgt dargestellt:
x[i] = m + Sum( a[h]*Cos(w[h]*i) + b[h]*Sin(w[h]*i), h=1..H )
Dabei gilt:
- x[i] - der Preis zum i-ten Balken, insgesamt n vergangene Preise;
- m - der Bias;
- a[h] und b[h] - Skalierungskoeffizienten der Harmoniken;
- w[h] - Frequenz einer harmonischen Schwingung;
- h - die harmonische Nummer;
- H - die Gesamtzahl der angepassten Harmoniken.
Das Anpassen dieses Modells bedeutet, m, a[h], b[h] und w[h] zu finden, sodass die modellierten Werte den realen Werten nahekommen. Die Bestimmung der harmonischen Frequenzen w[h] ist der schwierigste Teil des Anpassungsprozesses eines trigonometrischen Modells. Im Fall einer Fourier-Reihe werden diese Frequenzen auf 2*pi*h/n gesetzt. Die Fourier-Extrapolation bedeutet jedoch einfach, die n vergangenen Preise in die Zukunft zu wiederholen.
Dieser Indikator nutzt den Quinn-Fernandes-Algorithmus zur Bestimmung der harmonischen Frequenzen. Er passt die Harmoniken der trigonometrischen Reihe nacheinander an, bis die vorgegebene Gesamtzahl von Harmoniken H erreicht ist. Nach der Anpassung einer neuen Harmonischen berechnet der Algorithmus den Residuum zwischen dem aktualisierten Modell und den realen Werten und passt eine neue Harmonische an das Residuum an.
Der Indikator verfügt über folgende Eingabeparameter:
- Npast - Anzahl der vergangenen Balken, auf die die trigonometrische Reihe angepasst wird;
- Nfut - Anzahl der vorhergesagten zukünftigen Balken;
- Nharm - Gesamtzahl der Harmoniken im Modell;
- FreqTOL - Toleranz der Frequenzberechnungen.
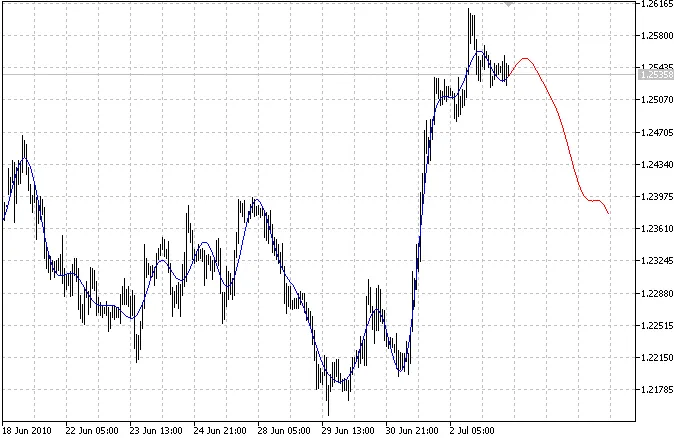
Der Indikator zeichnet zwei Kurven: Die blaue Kurve zeigt die modellierten vergangenen Werte an, während die rote Kurve die modellierten zukünftigen Werte darstellt.
Verwandte Beiträge
- Hull Moving Average: Ein unverzichtbarer Indikator für MetaTrader 5
- MA Cross Alert Once – Ein hilfreicher Indikator für MetaTrader 4
- Tägliche prozentuale Veränderung in MT4 – Indikator für MetaTrader 4
- Awesome_HTF_Signal: Ihr zuverlässiger Indikator für den MetaTrader 5
- Täglicher Drawdown: Ein wichtiger Indikator für MetaTrader 5
