Você já ouviu falar da extrapolação de Fourier? Esse modelo trigonômico, conhecido como multi-harmônico, é uma ferramenta poderosa para analisar séries de preços. Vamos entender como ele funciona e como você pode utilizá-lo no MetaTrader 5.
x[i] = m + Soma( a[h]*Cos(w[h]*i) + b[h]*Sin(w[h]*i), h=1..H )
Onde:
- x[i] - preço passado no i-ésimo candle, totalizando n preços passados;
- m - viés;
- a[h] e b[h] - coeficientes de escala das harmônicas;
- w[h] - frequência de uma harmônica;
- h - número da harmônica;
- H - total de harmônicas ajustadas.
Ajustar esse modelo significa encontrar os valores de m, a[h], b[h], e w[h] que aproximam os valores modelados dos valores reais. O maior desafio é descobrir as frequências harmônicas w[h]. No caso da série de Fourier, essas frequências são definidas como 2*pi*h/n. Contudo, a extrapolação de Fourier basicamente repete os n preços passados para prever o futuro.
Este indicador utiliza o algoritmo de Quinn-Fernandes para encontrar as frequências harmônicas. Ele ajusta as harmônicas da série trigonométrica uma a uma, até que o número total especificado de harmônicas H seja atingido. Após ajustar uma nova harmônica, o algoritmo computa o resíduo entre o modelo atualizado e os valores reais, ajustando uma nova harmônica ao resíduo.
Os parâmetros de entrada do indicador são os seguintes:
- Npast - número de candles passados aos quais a série trigonométrica é ajustada;
- Nfut - número de candles futuros previstos;
- Nharm - total de harmônicas no modelo;
- FreqTOL - tolerância para os cálculos de frequência.
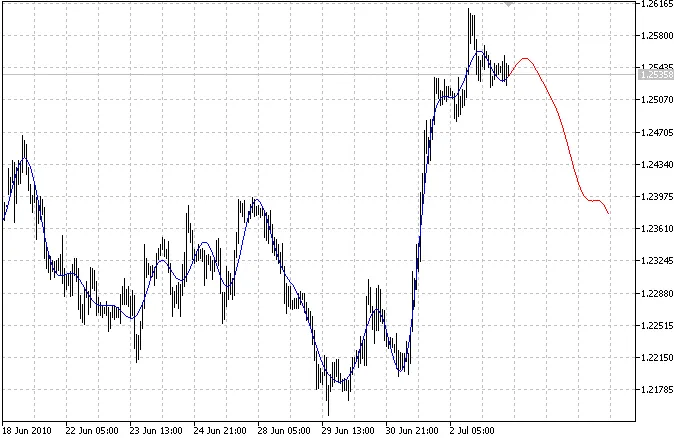
O indicador traça duas curvas: a curva azul representa os valores passados modelados e a curva vermelha indica os valores futuros modelados.
Publicações relacionadas
- iMFISignAlert: O Indicador para MetaTrader 5 que Gera Alertas
- Buffers Horários para Coleta de Dados no MetaTrader 5
- Calendário Econômico: Monitoramento e Cache para Testes de Estratégia no MetaTrader 5
- Pivot Point Personalizado com Horário de Fechamento Ajustável para MetaTrader 4
- Índice de Caminhada Aleatória: Um Indicador Essencial para MetaTrader 5
