Un modèle trigonométrique multi-harmonique (ou multi-ton) d'une série de prix x[i], avec i variant de 1 à n, se présente comme suit :
x[i] = m + Somme( a[h]*Cos(w[h]*i) + b[h]*Sin(w[h]*i), h=1..H )
où :
- x[i] - prix passé à la barre i, avec un total de n prix passés ;
- m - biais ;
- a[h] et b[h] - coefficients d'échelle des harmoniques ;
- w[h] - fréquence d'une harmonique ;
- h - numéro de l'harmonique ;
- H - nombre total d'harmoniques ajustées.
Ajuster ce modèle signifie trouver m, a[h], b[h], et w[h] de manière à ce que les valeurs modélisées soient proches des valeurs réelles. Trouver les fréquences harmoniques w[h] est la partie la plus complexe de l'ajustement d'un modèle trigonométrique. Dans le cas d'une série de Fourier, ces fréquences sont fixées à 2*pi*h/n. Cependant, l'extrapolation de la série de Fourier consiste simplement à reproduire les n prix passés dans le futur.
Cet indicateur utilise l'algorithme de Quinn-Fernandes pour déterminer les fréquences harmoniques. Il ajuste les harmoniques de la série trigonométrique une par une jusqu'à atteindre le nombre total d'harmoniques H spécifié. Après avoir ajusté une nouvelle harmonique, l'algorithme calcule le résidu entre le modèle mis à jour et les valeurs réelles, puis ajuste une nouvelle harmonique au résidu.
Les paramètres d'entrée de l'indicateur sont les suivants :
- Npast - nombre de barres passées auxquelles la série trigonométrique est ajustée ;
- Nfut - nombre de barres futures prédites ;
- Nharm - nombre total d'harmoniques dans le modèle ;
- FreqTOL - tolérance des calculs de fréquence.
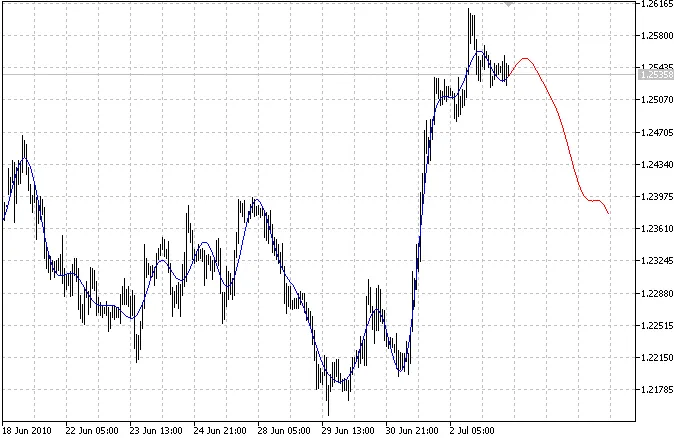
L'indicateur trace deux courbes : la courbe bleue indique les valeurs passées modélisées et la courbe rouge montre les valeurs futures modélisées.
Articles connexes
- iMAX3 : Détecteur de Tendances Rapides pour Traders
- Découvrez l'indicateur Tymen STARC Bands MTF pour MetaTrader 5
- Découvrez l'indicateur 3 en 1 Stochastic pour MetaTrader 5
- Affichez la tendance actuelle sur tous les délais avec un indicateur pour MetaTrader 4
- Améliorez vos graphiques avec ClearView : Indicateurs et modèles pour MetaTrader 5
