Un modello trigonometric multi-armonico (o multi-tono) di una serie di prezzi x[i], con i=1..n, è descritto dalla seguente formula:
x[i] = m + Somma(a[h]*Cos(w[h]*i) + b[h]*Sin(w[h]*i), h=1..H)
Dove:
- x[i] - prezzo passato alla barra i-esima, per un totale di n prezzi passati;
- m - bias;
- a[h] e b[h] - coefficienti di scala delle armoniche;
- w[h] - frequenza di un'armonica;
- h - numero dell'armonica;
- H - numero totale di armoniche adattate.
Adattare questo modello significa trovare m, a[h], b[h] e w[h] affinché i valori modellati siano vicini ai valori reali. Trovare le frequenze armoniche w[h] è la parte più complessa dell'adattamento di un modello trigonometrico. Nel caso di una serie di Fourier, queste frequenze sono impostate a 2*pi*h/n. Tuttavia, l'estrapolazione della serie di Fourier implica semplicemente la ripetizione dei n prezzi passati nel futuro.
Questo indicatore utilizza l'algoritmo di Quinn-Fernandes per determinare le frequenze armoniche. Adatta le armoniche della serie trigonometrica una per una fino a raggiungere il numero totale di armoniche H specificato. Dopo aver adattato una nuova armonica, l'algoritmo calcolato determina il residuo tra il modello aggiornato e i valori reali, quindi adatta una nuova armonica al residuo.
L'indicatore presenta i seguenti parametri di input:
- Npast - numero di barre passate a cui viene adattata la serie trigonometrica;
- Nfut - numero di barre future previste;
- Nharm - numero totale di armoniche nel modello;
- FreqTOL - tolleranza nei calcoli delle frequenze.
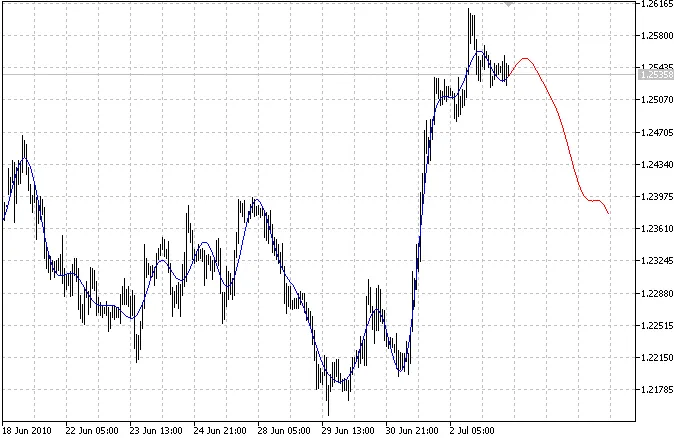
L'indicatore traccia due curve: la curva blu indica i valori passati modellati, mentre la curva rossa rappresenta i valori futuri modellati.
Post correlati
- Indicatori ZigZag Potenziati: Scopri le Nuove Funzionalità per MetaTrader 4
- Indice di Vigorità Relativa (RVI): Guida all'Utilizzo su MetaTrader 5
- HP Extrapolator: Scopri Come Ottimizzare le Previsioni con il Filtro Hodrick-Prescott
- Indice di Volatilità Chaikin: Scegli il Giusto Algoritmo di Smussamento per MetaTrader 5
- Indicatore Donchian Ultimate per MT4: Scopri tutte le Funzionalità
