HP Extrapolator: Scopri Come Ottimizzare le Previsioni con il Filtro Hodrick-Prescott

Autore: gpwr

Il filtro Hodrick-Prescott si distingue per la sua capacità di non introdurre ritardi nelle sue analisi. Questo filtro viene calcolato minimizzando la funzione obiettivo:

F = Somma((y[i] - x[i])^2,i=0..n-1) + lambda*Somma((y[i+1]+y[i-1]-2*y[i])^2,i=1..n-2)

dove x[] rappresenta i prezzi e y[] i valori del filtro. Di seguito, puoi vedere un esempio del comportamento di questo filtro (guarda il file HP.mq4 allegato).

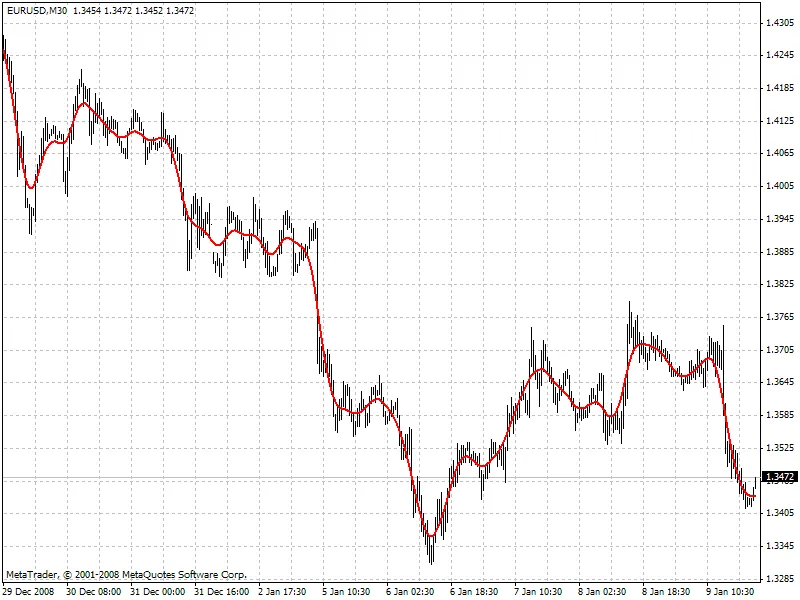
Se il filtro Hodrick-Prescott riesce a prevedere il futuro, quali valori futuri suggerisce? Per rispondere a questa domanda, dobbiamo trovare un filtro digitale a bassa frequenza con un parametro di frequenza simile a quello del filtro Hodrick-Prescott, ma con valori calcolati direttamente utilizzando i valori passati del "filtro gemello" stesso, cioè:

y[i] = Somma(a[k]*x[i-k],k=0..nx-1) - filtro FIR

oppure

y[i] = Somma(a[k]*x[i-k],k=0..nx-1) + Somma(b[k]*y[i-k],k=1..ny) - filtro IIR

È preferibile scegliere il "filtro gemello" con un ritardo Tdel indipendente dalla frequenza (ritardo di gruppo costante). I filtri IIR non sono adatti. Per i filtri FIR, la condizione per un ritardo indipendente dalla frequenza è la seguente:

a[i] = +/-a[nx-1-i], i = 0..nx-1

Il filtro FIR più semplice con ritardo costante è la Media Mobile Semplice (SMA):

y[i] = Somma(x[i-k],k=0..nx-1)/nx

Se nx è un numero dispari, Tdel = (nx-1)/2. Se spostiamo i valori del filtro SMA nel passato di un numero di barre pari a Tdel, i valori SMA coincidono con quelli del filtro Hodrick-Prescott. Tuttavia, non possiamo raggiungere una corrispondenza esatta a causa delle significative differenze nei parametri di frequenza dei due filtri (guarda il grafico qui sotto):

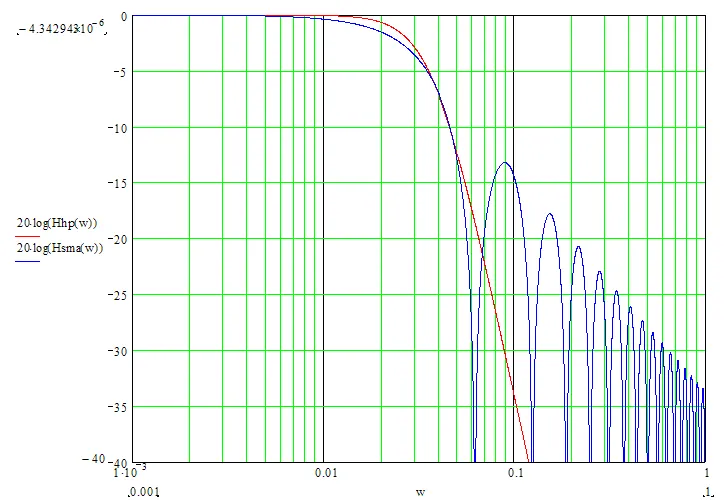
Per ottenere la corrispondenza più vicina tra i valori dei filtri, consiglio di mantenere larghezze di canale simili (ad esempio, -6dB). La larghezza del canale del filtro Hodrick-Prescott di -6dB è calcolata come segue:

wc = 2*arcsin(0.5/lambda^0.25).

La larghezza del canale di -6dB per il filtro SMA è calcolata tramite computazione numerica secondo la seguente equazione:

|H(w)| = sin(nx*wc/2)/sin(wc/2)/nx = 0.5

Il grafico qui sotto confronta i valori dei due filtri con larghezze di canale simili: rosso - filtro Hodrick-Prescott (FiltPer = 25), blu - SMA (Period = 15, Shift = -7). Nota che non ci sono dati SMA per le ultime 7 barre poiché ha bisogno di conoscere i prezzi futuri. Al contrario, il filtro Hodrick-Prescott (rosso) mostra alcuni valori. Se lo SMA spostato ripete i valori del filtro Hodrick-Prescott nelle ultime 7 barre dopo che i prezzi futuri appaiono, quali possono essere questi valori?

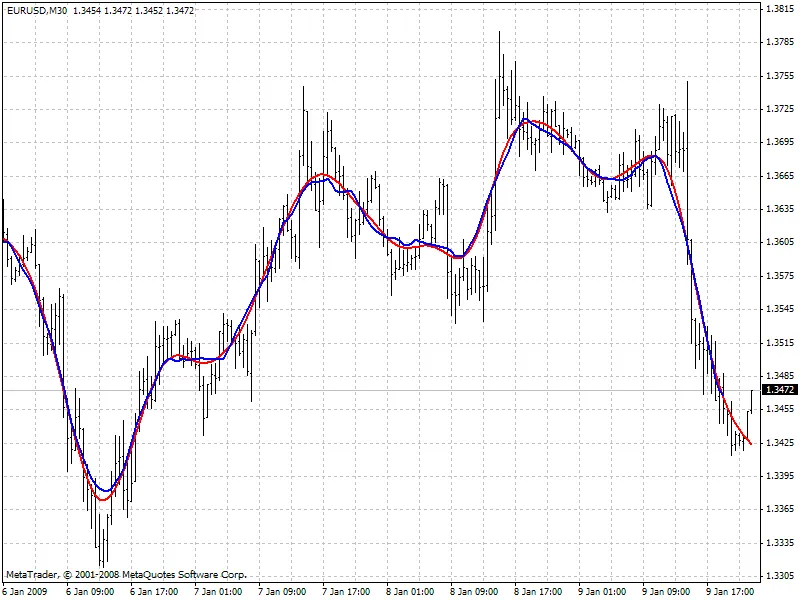
Algoritmi di previsione:

L'indicatore presenta due metodi di previsione:

Metodo 1:

• Imposta la lunghezza SMA a 3 e spostala nel passato di 1 barra. Con questa lunghezza, lo SMA spostato non esiste solo per l'ultima barra (Bar = 0), poiché ha bisogno del valore del prossimo prezzo futuro Close[-1].
• Calcola la larghezza del canale del filtro SMA. Eguagliala a quella del filtro Hodrick-Prescott. Trova lambda.
• Calcola il valore del filtro Hodrick-Prescott all'ultima barra HP[0] e assumi che SMA[0] con Close[-1] sconosciuto dia lo stesso valore.
• Trova Close[-1] = 3*HP[0] - Close[0] - Close[1]
• Aumenta la lunghezza dello SMA a 5. Ripeti tutti i calcoli e trova Close[-2] = 5*HP[0] - Close[-1] - Close[0] - Close[1] - Close[2]. Continua fino a calcolare il numero specificato di prezzi futuri FutBars.

Metodo 2:

• Imposta la lunghezza SMA uguale a 2*FutBars+1 e sposta lo SMA nel passato di FutBars.
• Calcola la larghezza del canale del filtro SMA. Eguagliala a quella del filtro Hodrick-Prescott. Trova lambda.
• Calcola i valori del filtro Hodrick-Prescott all'ultima FutBars e assumi che lo SMA si comporti in modo simile quando compaiono nuovi prezzi.
• Trova Close[-1] = (2*FutBars+1)*HP[FutBars-1] - Somma(Close[i],i=0..2*FutBars-1), Close[-2] = (2*FutBars+1)*HP[FutBars-2] - Somma(Close[i],i=-1..2*FutBars-2), ecc.

L'indicatore presenta i seguenti input:

• Metodo - metodo di previsione
• LastBar - numero dell'ultima barra su cui controllare le previsioni sui prezzi esistenti (LastBar >= 0)
• PastBars - numero di barre precedenti per cui viene calcolato il filtro Hodrick-Prescott (più sono, meglio è, o almeno PastBars > 2*FutBars)
• FutBars - numero di valori futuri previsti

L'indicatore evidenzia i valori previsti in rosso. Il Metodo 1 è utilizzato nell'esempio qui sotto:

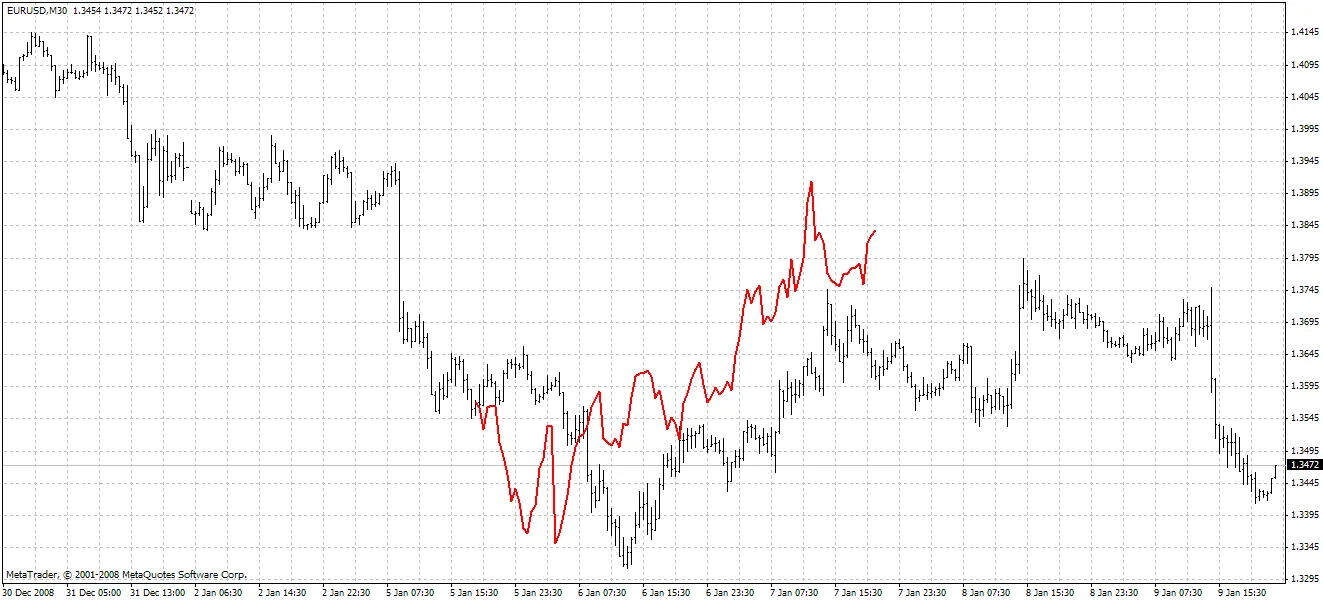
Metodo 2:

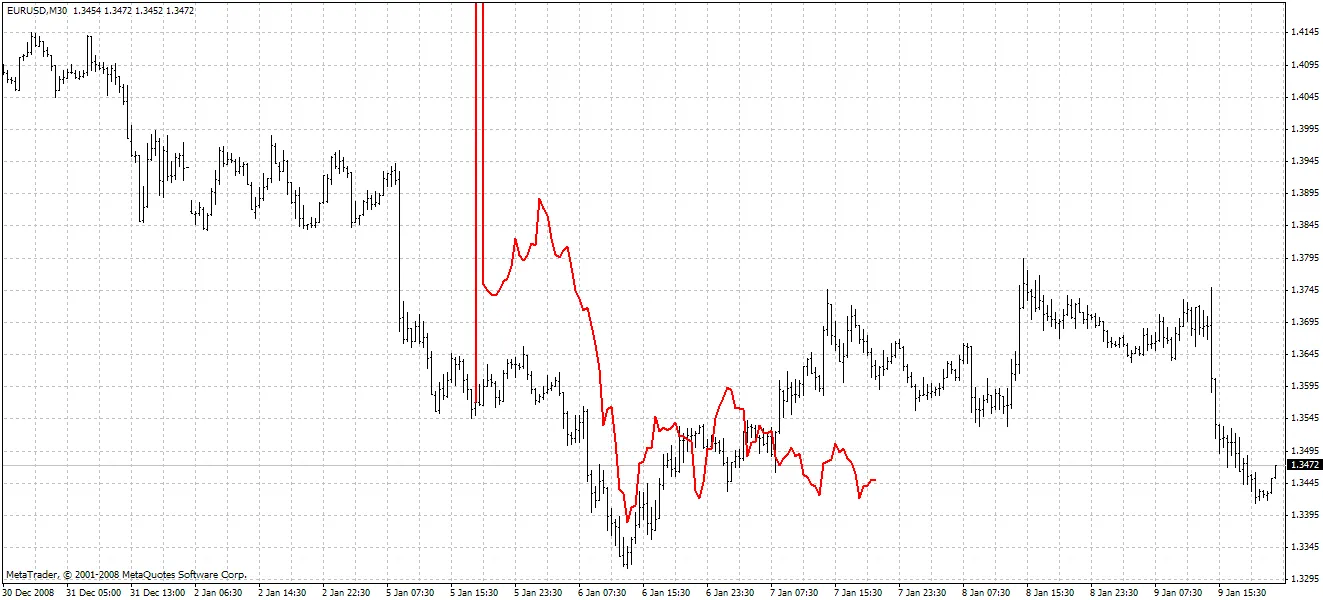
Il secondo metodo è più preciso ma spesso presenta picchi elevati nel primo prezzo previsto. Il metodo di previsione descritto può essere migliorato cercando un filtro FIR con il parametro di frequenza più vicino a quello del filtro Hodrick-Prescott. Ad esempio, puoi provare i filtri Hanning, Blackman, Kaiser e altri filtri a ritardo costante invece della SMA.

Un ringraziamento speciale all'utente Korey per l'indicatore originale del filtro Hodrick-Prescott pubblicato nella seguente sezione del Forum (in russo):

https://www.mql5.com/ru/forum/113677/page2