फॉरियर्स एक्सट्रापोलेशन एक मल्टी-हार्मोनिक (या मल्टी-टोन) त्रिकोणीय मॉडल है, जो एक मूल्य श्रृंखला x[i] को दर्शाता है, जहाँ i=1..n:
x[i] = m + Sum( a[h]*Cos(w[h]*i) + b[h]*Sin(w[h]*i), h=1..H )
जहाँ:
- x[i] - i-थ बार पर पिछले मूल्य, कुल n पिछले मूल्य;
- m - बायस;
- a[h] और b[h] - हार्मोनिक्स के स्केलिंग गुणांक;
- w[h] - एक हार्मोनिक की आवृत्ति;
- h - हार्मोनिक संख्या;
- H - समायोजित हार्मोनिक्स की कुल संख्या।
इस मॉडल को फिट करना मतलब है कि m, a[h], b[h], और w[h] को खोजना है जिससे कि मॉडल किए गए मान वास्तविक मानों के करीब हों। हार्मोनिक आवृत्तियों w[h] को खोजना इस त्रिकोणीय मॉडल को फिट करने का सबसे कठिन भाग है। फॉरियर्स श्रृंखला के मामले में, ये आवृत्तियाँ 2*pi*h/n पर सेट की जाती हैं। लेकिन, फॉरियर्स श्रृंखला का एक्सट्रापोलेशन का मतलब सिर्फ पिछले n मूल्यों को भविष्य में दोहराना है।
यह संकेतक क्विन-फर्नांडेस एल्गोरिदम का उपयोग करके हार्मोनिक आवृत्तियों को खोजता है। यह ट्रिगोनोमेट्रिक श्रृंखला के हार्मोनिक्स को एक-एक करके फिट करता है जब तक कि निर्दिष्ट कुल हार्मोनिक्स H तक नहीं पहुँच जाता। एक नया हार्मोनिक फिट करने के बाद, कोडेड एल्गोरिदम अद्यतन मॉडल और वास्तविक मानों के बीच अवशेष की गणना करता है और अवशेष के लिए एक नया हार्मोनिक फिट करता है।
इस संकेतक के निम्नलिखित इनपुट पैरामीटर हैं:
- Npast - पिछले बार की संख्या, जिसके लिए ट्रिगोनोमेट्रिक श्रृंखला को फिट किया जाता है;
- Nfut - भविष्य के अनुमानित बार की संख्या;
- Nharm - मॉडल में कुल हार्मोनिक्स;
- FreqTOL - आवृत्ति गणनाओं की सहिष्णुता।
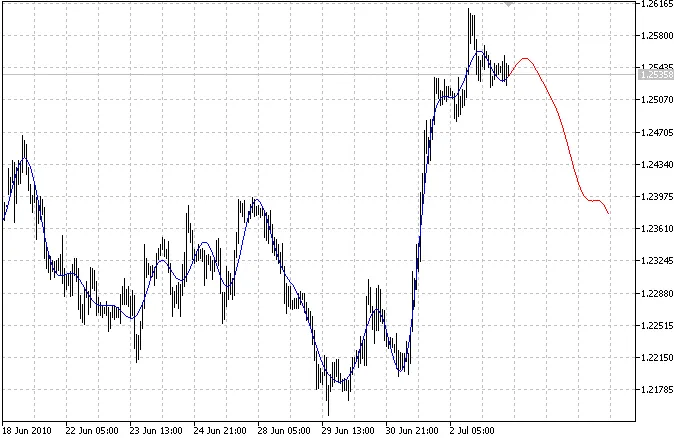
संकेतक दो वक्रों को प्लॉट करता है: नीली वक्र पिछले मॉडल किए गए मानों को दर्शाती है और लाल वक्र मॉडल किए गए भविष्य के मानों को दर्शाती है।