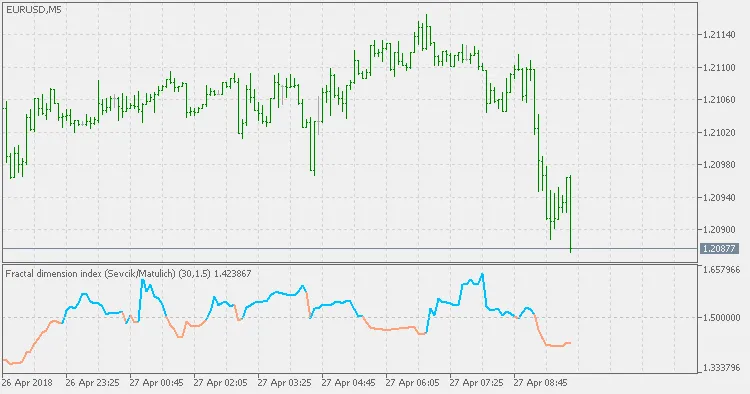
फ्रैक्टल डाइमेंशन इंडेक्स (FDI) की व्याख्या के अनुसार:
मंडेलब्रोट ने फ्रैक्टल डाइमेंशन इंडेक्स (FDI) को इस तरह से परिभाषित किया है कि यह मापता है कि "कितना जटिल और अनियमित" कुछ है। FDI का उपयोग शेयर बाजार में संकेतक के रूप में किया जा सकता है।
हम बाजार में कीमतों को "ट्रेंडिंग" या "रेंजिंग" के रूप में देख सकते हैं। जब एक मजबूत रैली होती है, तो कीमतें तेज़ी से बढ़ती हैं, कभी-कभी एक आयामी सीधी रेखा के करीब पहुँच जाती हैं। और अगर हम मानते हैं कि कीमतों को एक अधिक खुरदुरी फ्रैक्टल पैटर्न में चलना चाहिए, तो हम मानेंगे कि लगभग सीधी गति किसी बिंदु पर समाप्त होगी जिसे हम एक उचित ट्रेड करने के लिए एक निश्चित सटीकता के साथ भविष्यवाणी कर सकते हैं।
ट्रेंडिंग के बाद, कीमतें अक्सर कुछ समय के लिए एक रेंज में व्यापार करती हैं इससे पहले कि वे अगले ट्रेंड की ओर बढ़ें। कल्पना करें कि कीमतें एक आयताकार पैटर्न में व्यापार कर रही हैं, दो-आयामी प्लेन पैटर्न में एक ही बिंदुओं पर आगे-पीछे झूल रही हैं। एक प्लेन न तो एक फ्रैक्टल है और न ही एक सीधी रेखा, इसलिए हम उम्मीद कर सकते हैं कि कीमतें रेंज से बाहर निकल जाएँगी और फिर से एक फ्रैक्टल की तरह व्यवहार करेंगी।
इसलिए, FDI एक ऐसा तरीका है जो आपके चार्ट पर रेखा को एक संख्या सौंपता है। यह संख्या 1.0 और 2.0 के बीच होगी। जितनी अधिक कीमतें एक आयामी सीधी रेखा के करीब होंगी, उतना ही FDI 1.0 के करीब चलेगा। और जितनी अधिक कीमतें एक दो-आयामी प्लेन से मिलती-जुलती होंगी, उतना ही FDI 2.0 के करीब चलेगा।
यह संस्करण मूल FDI के आविष्कारक (कार्लोस सेव्सिक) द्वारा वर्णित के अनुसार बनाया गया है, एक सुधार के साथ: सेव्सिक द्वारा प्रकाशित सूत्र उलटा था। इस गलती को एलेक्स मातुलिच ने सही किया और यह संस्करण सही गणना का उपयोग कर रहा है।