บทนำ
ในโลกของการเทรด มีโปรแกรมมากมายที่ช่วยให้เราสร้างเซ็ทที่คล้ายกันได้ เช่น ระบบฟังก์ชันที่ทำซ้ำ (IFS) อย่างเช่น Fractint, Fractal Designer หรือ IFS Matlab Generator จากความเร็วของ ภาษา MQL5 และความสามารถในการทำงานกับวัตถุกราฟิก ทำให้เราสามารถศึกษาชุดที่สวยงามเหล่านี้ได้ใน MetaTrader 5 ได้อย่างง่ายดาย
ไลบรารี cIntBMP ที่พัฒนาโดย Dmitry (Integer) มอบโอกาสใหม่ในการสร้างกราฟิก และทำให้การสร้างภาพกราฟิกนั้นง่ายขึ้นมาก ไลบรารีนี้ยังได้รับรางวัลพิเศษจาก MetaQuotes Software Corp.
ในบทความนี้เราจะมาพิจารณาตัวอย่างการทำงานกับไลบรารี cIntBMP และจะพูดถึงอัลกอริธึมในการสร้างชุดฟรัคทัลโดยใช้ระบบฟังก์ชันที่ทำซ้ำ
1. การแปลงอาฟฟินของระนาบ
การแปลงอาฟฟินของระนาบคือการแมพ 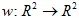 โดยทั่วไป การแปลง 2D อาฟฟินสามารถกำหนดได้ด้วย
โดยทั่วไป การแปลง 2D อาฟฟินสามารถกำหนดได้ด้วย 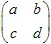 เมทริกซ์ และ
เมทริกซ์ และ 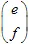 เวกเตอร์ จุดที่มีพิกัด (x,y) จะถูกแปลงไปยังจุดอื่น
เวกเตอร์ จุดที่มีพิกัด (x,y) จะถูกแปลงไปยังจุดอื่น 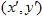 โดยใช้การแปลงเชิงเส้น:
โดยใช้การแปลงเชิงเส้น:
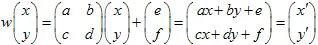
การแปลงนี้ต้องไม่เป็นศูนย์, 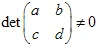 . การแปลงอาฟฟินจะเปลี่ยนขนาด
. การแปลงอาฟฟินจะเปลี่ยนขนาด 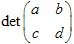 เท่า.
เท่า.
การแปลงอาฟฟินไม่เปลี่ยนโครงสร้างของวัตถุทางเรขาคณิต (เส้นที่ถูกแปลงเป็นเส้น) AT ช่วยให้เราสามารถอธิบาย "การบิดเบือน" ง่าย ๆ ของวัตถุ เช่น การหมุน, การขยาย และการแปล
ตัวอย่างของการแปลงอาฟฟิน:
1) การหมุนของระนาบ ที่มุม:
2) "การขยาย" ของระนาบด้วย
และ
ค่าสัมประสิทธิ์ (แกน X และ Y):
3) การแปล ของระนาบโดย
เวกเตอร์:
การ ทำซ้ำการหดตัว คือกุญแจสำคัญ (ดู ผลลัพธ์ของ Hutchinson).
หาก 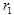 และ
และ 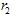 มีพิกัด
มีพิกัด 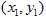 และ
และ 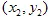 และ
และ 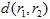 เป็นมาตรฐาน (เช่น มาตรฐานยูคลิด:
เป็นมาตรฐาน (เช่น มาตรฐานยูคลิด: 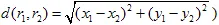 ). การแปลงอาฟฟินเรียกว่าการ หดตัว หาก
). การแปลงอาฟฟินเรียกว่าการ หดตัว หาก 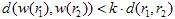 , ที่ไหน
, ที่ไหน 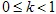 .
.
นี่คือตัวอย่างของการแปลงอาฟฟิน:

ผลลัพธ์คือ:
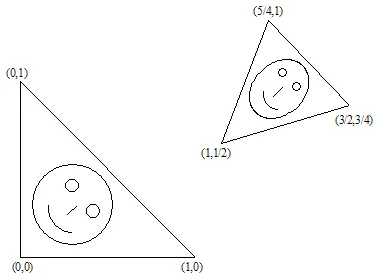
2. การแปลงความคล้ายคลึง
ฟรัคทัลถูกสร้างขึ้นโดยวิธีดังต่อไปนี้: วัตถุทางเรขาคณิต (ส่วน, สามเหลี่ยม, สี่เหลี่ยม) แบ่งออกเป็น N ชิ้น และ M ของพวกมันถูกใช้ในการ "สร้าง" ชุดต่อไป (หาก N=M เราจะได้มิติจำนวนเต็มของชุดที่เกิดขึ้น). นอกจากนี้ กระบวนการนี้จะถูกทำซ้ำอีกครั้งและอีกครั้งสำหรับแต่ละชิ้น.
ฟรัคทัลคลาสสิก:
ส่วน:
- Triadic Koch Curve, N=3, M=4;
- Cantor Dust, N=3, M=2;
สามเหลี่ยม:
- Sierpinski Gasket, N=4, M=3;
สี่เหลี่ยม:
- Sierpinski Carpet, N=9, M=8;
- Vichek fractal, N=9, M=5.
และอื่น ๆ.
ฟรัคทัลมีโครงสร้างที่คล้ายกันเอง บางส่วนสามารถกำหนดได้โดยการทำซ้ำความคล้ายคลึงกันหลายครั้ง โครงสร้างของการแปลงอาฟฟินขึ้นอยู่กับวิธีการสร้างฟรัคทัล.
ตามที่คุณจะเห็นต่อไป มันง่ายมาก และปัญหาเดียวที่เราต้องแก้ไขคือการอธิบายเพียงการทำซ้ำแรกของการสร้างฟรัคทัลและค้นหาชุดการแปลงอาฟฟินที่เกี่ยวข้อง.
สมมติว่าเรามีชุดหนึ่ง ตามอัลกอริธึมการสร้างฟรัคทัล เราจำเป็นต้องลดมัน, หมุน และ "วางในตำแหน่งที่แน่นอน". ปัญหาคือการอธิบายกระบวนการนี้โดยใช้การแปลงอาฟฟิน นั่นคือเราต้องหาค่าเมทริกซ์และเวกเตอร์.
มันง่ายที่จะพิสูจน์ว่าเพียงพอที่จะใช้ 3 จุดของชุดเริ่มต้น (ที่ไม่ใช่ศูนย์) และแปลงพวกเขาไปยัง 3 จุดที่เกี่ยวข้องของชุด "ที่ลดลง". การแปลงนี้จะนำไปสู่สมการเชิงเส้น 6 สมการที่ทำให้เราสามารถหาค่า a,b,c,d,e,f เป็นคำตอบ.
มาดูกันว่ามันทำงานอย่างไร สมมติว่า 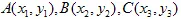 สามเหลี่ยมถูกแปลงไปยัง
สามเหลี่ยมถูกแปลงไปยัง 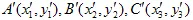 สามเหลี่ยม.
สามเหลี่ยม.
โดยการแก้ไขระบบสมการเชิงเส้นเราจะสามารถหาค่า a,b,c,d,e และ f:
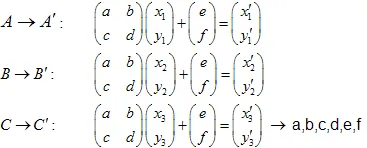
ตัวอย่าง:Sierpinski Gasket:
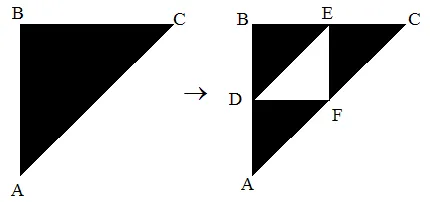
พิกัดของจุดคือ:
- A (0,0)
- B (0,1)
- C (1,1)
- D(0,1/2)
- E (1/2,1)
- F(1/2,1/2)
เรามี 3 การแปลง:
- ABC -> ADF
- ABC -> DBE
- ABC -> FEC
ระบบสมการเชิงเส้นมีลักษณะดังนี้:
คำตอบคือ:  ,
, 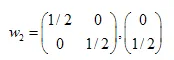 ,
, 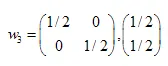
เราพบค่าของการแปลงอาฟฟิน 3 อย่างแล้ว ต่อไปเราจะใช้เพื่อสร้างชุดที่คล้ายกันเอง.
3. การสร้างฟรัคทัลโดยใช้ระบบฟังก์ชันที่ทำซ้ำ
ระบบฟังก์ชันที่ทำซ้ำ (IFS) เป็นชุดของการหดตัวอาฟฟิน 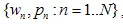 โดยที่
โดยที่ 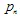 - เป็น "น้ำหนัก". ฟังก์ชันแต่ละฟังก์ชันของ IFS ถูกกำหนดโดยตัวเลข 7 ตัว:
- เป็น "น้ำหนัก". ฟังก์ชันแต่ละฟังก์ชันของ IFS ถูกกำหนดโดยตัวเลข 7 ตัว: 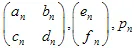 , โดยที่
, โดยที่ 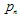 น้ำหนักจะถูกใช้เมื่อกระบวนการทำซ้ำในฐานะความน่าจะเป็นของการแปลง n-th. ควรกำหนดค่าของพวกเขาตามสัดส่วนกับการหดตัว:
น้ำหนักจะถูกใช้เมื่อกระบวนการทำซ้ำในฐานะความน่าจะเป็นของการแปลง n-th. ควรกำหนดค่าของพวกเขาตามสัดส่วนกับการหดตัว: 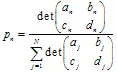 .
.
มาพิจารณาอัลกอริธึมในการสร้างฟรัคทัลโดยใช้ระบบฟังก์ชันที่ทำซ้ำ (ดูเพิ่มเติมที่ Chaos Game).
ขั้นแรกเราต้องเลือกจุดเริ่มต้นบางจุดโดยมีพิกัด 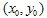 . ถัดไปเราจะเลือกการหดตัวที่เลือกแบบสุ่มและวางจุด
. ถัดไปเราจะเลือกการหดตัวที่เลือกแบบสุ่มและวางจุด 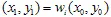 . และอีกครั้ง เราจะเลือกการหดตัวที่เลือกแบบสุ่ม
. และอีกครั้ง เราจะเลือกการหดตัวที่เลือกแบบสุ่ม 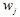 และวาง
และวาง 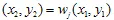 . สุดท้ายเราจะได้
. สุดท้ายเราจะได้ 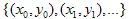 เป็นชุดของจุด.
เป็นชุดของจุด.
การเลือกการหดตัวขึ้นอยู่กับความน่าจะเป็นของมัน. หากเราทำซ้ำกระบวนการ (เช่น ใช้จุด ~30000 จุด) และวางชุดที่ได้ เราจะเห็นโครงสร้างของมันแม้ว่าจะเป็นกระบวนการสุ่ม.
นี่คือตัวอย่างของ Sierpinski Gasket:
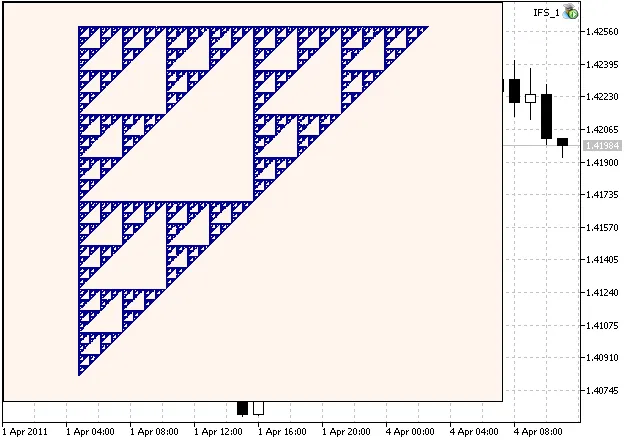
Figure 1. The Sierpinski Gasket, generated with IFS coefficients calculated in chapter 2
รหัส:
//+------------------------------------------------------------------+//| IFS_Sierpinski_Gasket.mq5 |//| Copyright 2011, MetaQuotes Software Corp. |//| https://www.mql5.com |//+------------------------------------------------------------------+#property copyright "Copyright 2011, MetaQuotes Software Corp."#property link "https://www.mql5.com"#property version "1.00"//-- include file with cIntBMP class#include <cIntBMP.mqh>//-- Sierpinski Gasket IFS coefficients//-- (a,b,c,d) matriciesdouble IFS_a[3] = {0.50, 0.50, 0.50}; double IFS_b[3] = {0.00, 0.00, 0.00}; double IFS_c[3] = {0.00, 0.00, 0.00}; double IFS_d[3] = {0.50, 0.50, 0.50}; //-- (e,f) vectorsdouble IFS_e[3] = {0.00, 0.00, 0.50}; double IFS_f[3] = {0.00, 0.50, 0.50}; //-- "probabilities" of transforms, multiplied by 1000double IFS_p[3]={333,333,333}; double Probs[3]; // Probs array - used to choose IFS transforms cIntBMP bmp; // cIntBMP class instanceint scale=350; // scale coefficient//+------------------------------------------------------------------+//| Expert initialization function |//+------------------------------------------------------------------+intOnInit() { //-- Prepare Probs array double m=0; for(int i=0; i<ArraySize(IFS_p); i++) { Probs[i]=IFS_p[i]+m; m=m+IFS_p[i]; } //-- size of BMP image int XSize=500; int YSize=400; //-- create bmp image XSizexYSize with clrSeashell background color bmp.Create(XSize,YSize,clrSeashell); //-- image rectangle bmp.DrawRectangle(0,0,XSize-1,YSize-1,clrBlack); //-- point coordinates (will be used in construction of set) double x0=0; double y0=0; double x,y; //-- number of points to calculate (more points - detailed image) int points=1500000; //-- calculate set for(int i=0; i<points; i++) { // choose IFS tranform with probabilities, proportional to defined double prb=1000*(rand()/32767.0); for(int k=0; k<ArraySize(IFS_p); k++) { if(prb<=Probs[k]) { // affine transformation x = IFS_a[k] * x0 + IFS_b[k] * y0 + IFS_e[k]; y = IFS_c[k] * x0 + IFS_d[k] * y0 + IFS_f[k]; // update previous coordinates x0 = x; y0 = y; // convert to BMP image coordinates // (note the Y axis in cIntBMP) int scX = int (MathRound(XSize/2 + (x-0.5)*scale)); int scY = int (MathRound(YSize/2 + (y-0.5)*scale)); // if the point coordinates inside the image, draw the dot if(scX>=0 && scX<XSize && scY>=0 && scY<YSize) { bmp.DrawDot(scX,scY,clrDarkBlue); } break; } } } //-- save image to file bmp.Save("bmpimg",true); //-- plot image on the chart bmp.Show(0,0,"bmpimg","IFS"); //--- return(0); } //+------------------------------------------------------------------+//| Expert deinitialization function |//+------------------------------------------------------------------+voidOnDeinit(constint reason) { //--- delete image from the chart ObjectDelete(0,"IFS"); //--- delete file bmp.Delete("bmpimg",true); } //+------------------------------------------------------------------+
หากเรากำหนดค่า scale เป็น 1350, เพิ่มจำนวนการทำซ้ำเป็น 15000000 และเปลี่ยนตำแหน่งจุดเริ่มต้น:
int scX = MathRound(XSize/2 + (x-0.75)*scale); int scY = MathRound(YSize/2 + (y-0.75)*scale);
เราจะสามารถเห็นส่วนที่ซูมของชุดได้ หนึ่งสามารถเห็น (รูปที่ 2) ว่ามันมีโครงสร้างที่คล้ายกันเอง:
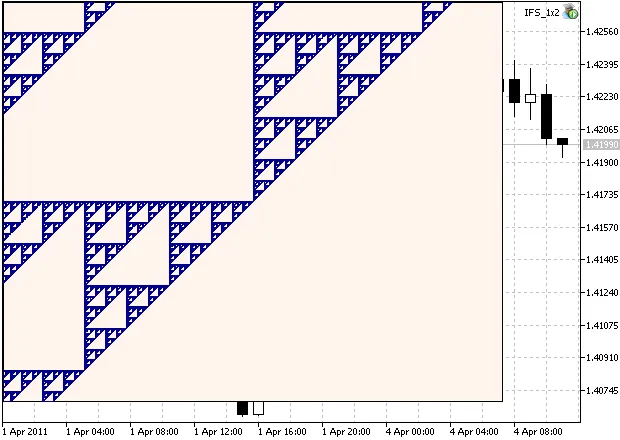
Figure 2. Zoomed region of Sierpinski Gasket
มาพิจารณาฟรัคทัลที่มีชื่อเสียง Barnsley's Fern, ที่เสนอโดย Michael Barnsley. มันซับซ้อนมากขึ้น.

Figure 3. Barnsley's Fern
รหัสจะคล้ายกัน แต่ในกรณีนี้เรามีการหดตัว IFS 4 ชนิดที่มีน้ำหนักต่างกัน.
//+------------------------------------------------------------------+//| IFS_fern.mq5 |//| Copyright 2011, MetaQuotes Software Corp. |//| https://www.mql5.com |//+------------------------------------------------------------------+#property copyright "Copyright 2011, MetaQuotes Software Corp."#property link "https://www.mql5.com"#property version "1.00"#include <cIntBMP.mqh>//-- Barnsley Fern IFS coefficients//-- (a,b,c,d) matriciesdouble IFS_a[4] = {0.00, 0.85, 0.20, -0.15}; double IFS_b[4] = {0.00, 0.04, -0.26, 0.28}; double IFS_c[4] = {0.00, -0.04, 0.23, 0.26}; double IFS_d[4] = {0.16, 0.85, 0.22, 0.24}; //-- (e,f) vectorsdouble IFS_e[4] = {0.00, 0.00, 0.00, 0.00}; double IFS_f[4] = {0.00, 1.60, 1.60, 0.00}; //-- "probabilities" of transforms, multiplied by 1000double IFS_p[4] = {10, 850, 70, 70}; double Probs[4]; cIntBMP bmp; int scale=50; //+------------------------------------------------------------------+//| Expert initialization function |//+------------------------------------------------------------------+intOnInit() { double m=0; for(int i=0; i<ArraySize(IFS_p); i++) { Probs[i]=IFS_p[i]+m; m=m+IFS_p[i]; } int XSize=600; int YSize=600; bmp.Create(XSize,YSize,clrSeashell); bmp.DrawRectangle(0,0,XSize-1,YSize-1,clrBlack); double x0=0; double y0=0; double x,y; int points=250000; for(int i=0; i<points; i++) { double prb=1000*(rand()/32767.0); for(int k=0; k<ArraySize(IFS_p); k++) { if(prb<=Probs[k]) { x = IFS_a[k] * x0 + IFS_b[k] * y0 + IFS_e[k]; y = IFS_c[k] * x0 + IFS_d[k] * y0 + IFS_f[k]; x0 = x; y0 = y; int scX = int (MathRound(XSize/2 + (x)*scale)); int scY = int (MathRound(YSize/2 + (y-5)*scale)); if(scX>=0 && scX<XSize && scY>=0 && scY<YSize) { bmp.DrawDot(scX,scY,clrForestGreen); } break; } } } bmp.Save("bmpimg",true); bmp.Show(0,0,"bmpimg","IFS"); //--- return(0); } //+------------------------------------------------------------------+//| Expert deinitialization function |//+------------------------------------------------------------------+voidOnDeinit(constint reason) { //-- delete image from the chart ObjectDelete(0,"IFS"); //-- delete file bmp.Delete("bmpimg",true); } //+------------------------------------------------------------------+
น่าสนใจว่าการสร้างโครงสร้างที่ซับซ้อนเช่นนี้สามารถกำหนดได้ด้วยตัวเลขเพียง 28 ตัว.
หากเราขยายสเกลเป็น 150 และกำหนดจำนวนรอบเป็น 1250000 เราจะเห็นส่วนที่ซูมของฟรัคทัล:
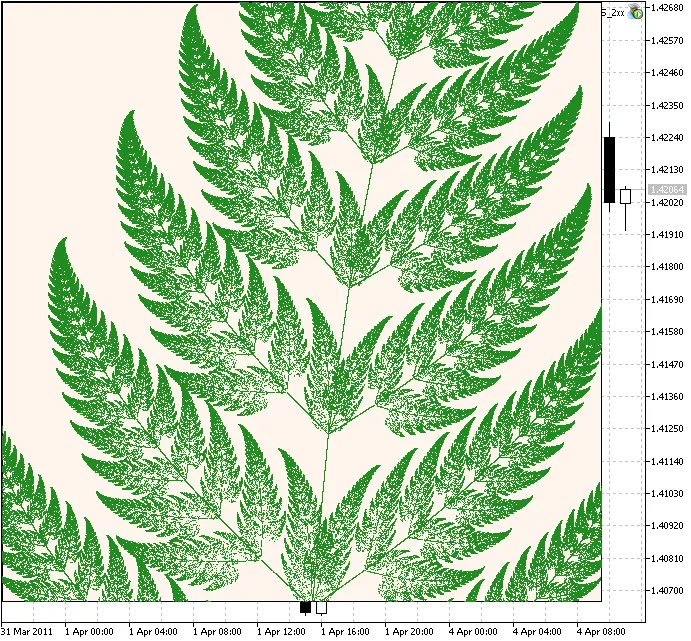
Figure 4. A fragment of Barnsley's Fern
ตามที่คุณเห็น อัลกอริธึมนี้เป็นสากล มันช่วยให้คุณสร้างชุดฟรัคทัลที่แตกต่างกัน.
ตัวอย่างถัดไปคือ Sierpinski Carpet ซึ่งกำหนดโดยค่าสัมประสิทธิ์ IFS ต่อไปนี้:
//-- Sierpinski Gasket IFS coefficientsdouble IFS_a[8] = {0.333, 0.333, 0.333, 0.333, 0.333, 0.333, 0.333, 0.333}; double IFS_b[8] = {0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00}; double IFS_c[8] = {0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00}; double IFS_d[8] = {0.333, 0.333, 0.333, 0.333, 0.333, 0.333, 0.333, 0.333}; double IFS_e[8] = {-0.125, -3.375, -3.375, 3.125, 3.125, -3.375, -0.125, 3.125}; double IFS_f[8] = {6.75, 0.25, 6.75, 0.25, 6.75, 3.5, 0.25, 3.50}; //-- "probabilities", multiplied by 1000double IFS_p[8]={125,125,125,125,125,125,125,125};
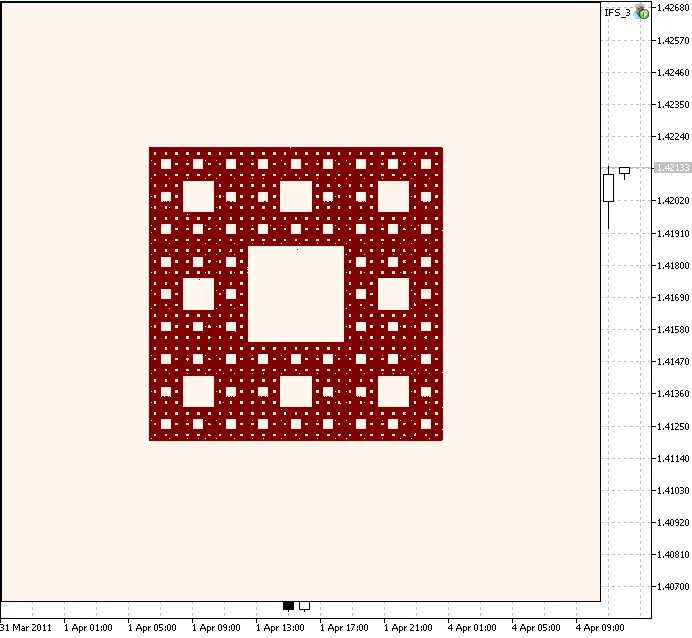
Figure 5. Sierpinski Carpet
ในบทที่ 2 เราได้พิจารณาอัลกอริธึมในการคำนวณค่าของการหดตัว IFS.
ลองสร้าง "คำฟรัคทัล" กันดู ในภาษารัสเซีย คำว่า "ฟรัคทัล" มีลักษณะดังนี้:
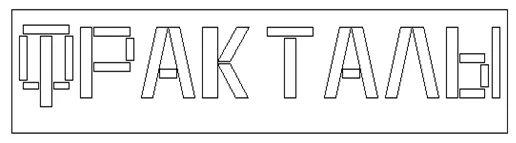
Figure 6. "Fractals" word in Russian
ในการหาค่าของ IFS เราต้องแก้ระบบเชิงเส้นที่เกี่ยวข้อง คำตอบคือ:
//-- IFS coefficients of the 
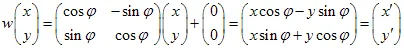
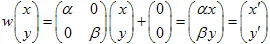
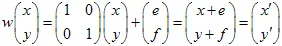
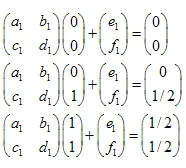

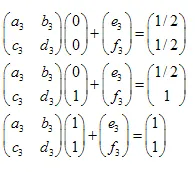
ความคิดเห็น 0