होम सिस्टम ट्रेडिंग पोस्ट

MQL5 में IFS का उपयोग कर फ्रैक्टल कैसे बनाएं - MetaTrader 5 के लिए

Mike • 2011-04-15 03:35
2 0 0

परिचय

फ्रैक्टल सेट बनाने के लिए कई प्रोग्राम हैं, जो Iterated Function System (IFS) द्वारा परिभाषित होते हैं। उदाहरण के लिए, Fractint, Fractal Designer, या IFS Matlab Generator। MQL5 भाषा की गति और ग्राफिकल ऑब्जेक्ट्स के साथ काम करने की क्षमता के कारण, ये खूबसूरत सेट MetaTrader 5 क्लाइंट टर्मिनल में अध्ययन किए जा सकते हैं।

cIntBMP पुस्तकालय, जिसे Dmitry (Integer) द्वारा विकसित किया गया है, नए ग्राफिकल अवसर प्रदान करता है और ग्राफिकल इमेज बनाने की प्रक्रिया को बहुत आसान बनाता है। इस पुस्तकालय को MetaQuotes Software Corp द्वारा विशेष पुरस्कार से सम्मानित किया गया था।

इस प्रकाशन में हम cIntBMP पुस्तकालय के साथ काम करने के उदाहरणों पर विचार करेंगे। इसके अलावा, हम Iterated Function Systems का उपयोग करके फ्रैक्टल सेट बनाने के एल्गोरिदम को भी कवर करेंगे।


1. समतल का एफ़ाइन ट्रांसफॉर्मेशन

समतल का एफ़ाइन ट्रांसफॉर्मेशन एक मैपिंग है 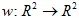। सामान्यतः, एफ़ाइन 2-डी ट्रांसफॉर्म को कुछ 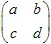मैट्रिक्स और 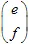वेक्टर के साथ परिभाषित किया जा सकता है। बिंदु (x,y) को कुछ अन्य बिंदु 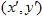में रूपांतरित किया जाता है:

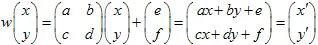
यह ट्रांसफॉर्मेशन गैर-विशिष्ट होना चाहिए, 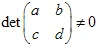। एफ़ाइन ट्रांसफॉर्म आकार को 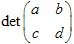गुना बदलता है।

एफ़ाइन ट्रांसफॉर्म जियोमेट्रिक वस्तुओं की संरचना को नहीं बदलता है (रेखाएँ रेखाओं में परिवर्तित होती हैं), एटी सरल "विकृति" का वर्णन करने की अनुमति देता है, जैसे कि घूर्णन, पैमाना और अनुवाद।

एफ़ाइन समतल ट्रांसफॉर्म का उदाहरण:

1) समतल का घूर्णन पर कोण:

2) "पैमाना" एक समतल का और गुणांक (X और Y अक्ष):

3) अनुवाद समतल द्वारा वेक्टर:

संकुचन के मानचित्र कुंजी हैं (देखें Hutchinson के परिणाम)।

यदि 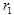और 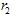के पास निर्देशांक 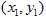और 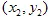हैं और 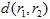एक मीट्रिक है (उदाहरण के लिए, यूक्लिड मीट्रिक: 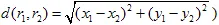)। एफ़ाइन ट्रांसफॉर्मेशन को संकुचन कहा जाता है यदि 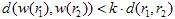, जहां ।

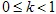यहाँ एफ़ाइन ट्रांसफॉर्मेशन का एक उदाहरण है:

परिणाम है:


2. समानता ट्रांसफॉर्म

फ्रैक्टल इस तरीके से बनाए जाते हैं: कुछ (सरल) जियोमेट्रिक ऑब्जेक्ट (सेक्शन, त्रिकोण, वर्ग) को N टुकड़ों में विभाजित किया जाता है और उनमें से M का उपयोग आगे के सेट के "निर्माण" के लिए किया जाता है (यदि N=M, तो हमें परिणामस्वरूप सेट का पूर्णांक आयाम मिलता है)। आगे यह प्रक्रिया बार-बार प्रत्येक टुकड़े के लिए दोहराई जाती है।

क्लासिक फ्रैक्टल:

सेक्शन:

  • ट्रायडिक कोच वक्र, N=3, M=4;
  • कैंटर डस्ट, N=3, M=2;

त्रिकोण:

  • सिरपिंस्की गास्केट, N=4, M=3;

वर्ग:

  • सिरपिंस्की कार्पेट, N=9, M=8;
  • विचेक फ्रैक्टल, N=9, M=5.

और इसी तरह।

फ्रैक्टल में आत्म-समरूप संरचना होती है, उनमें से कुछ को कई समानता ट्रांसफॉर्मेशन द्वारा परिभाषित किया जा सकता है। एफ़ाइन ट्रांसफॉर्म की संरचना फ्रैक्टल निर्माण के तरीके पर निर्भर करती है।

जैसा कि आप आगे देखेंगे, यह बहुत सरल है, और हमें जो एकमात्र समस्या हल करनी है वह है फ्रैक्टल निर्माण का केवल पहला पुनरावृत्ति का वर्णन करना और संबंधित सेट के एफ़ाइन ट्रांसफॉर्म्स को खोजना।

मान लें कि हमारे पास कुछ सेट है। फ्रैक्टल निर्माण के एल्गोरिदम के अनुसार, हमें इसे कम करना है, घुमाना है और "किसी निश्चित स्थान पर रखना है"। समस्या है कि इस प्रक्रिया का वर्णन एफ़ाइन ट्रांसफॉर्मेशन का उपयोग करके करना है, यानी हमें मैट्रिक्स और वेक्टर खोजना है।

यह आसानी से साबित किया जा सकता है कि प्रारंभिक सेट के 3 बिंदुओं को लेना पर्याप्त है (गैर-तुच्छ) और उन्हें "कम किए गए" सेट के 3 संबंधित बिंदुओं में परिवर्तित करना। यह ट्रांसफॉर्मेशन 6 रैखिक समीकरणों की ओर ले जाएगा, जिससे हमें a,b,c,d,e,f को समाधान के रूप में खोजना होगा।

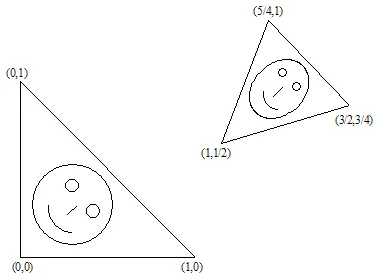
आइए इसे दिखाते हैं। मान लीजिए 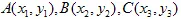त्रिकोण को 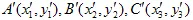त्रिकोण में परिवर्तित किया गया है।

रैखिक समीकरणों के इस प्रणाली को हल करके हम a,b,c,d,e और f गुणांक प्राप्त कर सकते हैं:

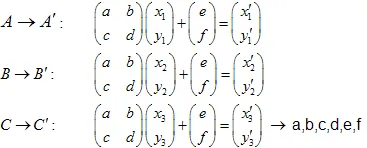
उदाहरण: सिरपिंस्की गास्केट:

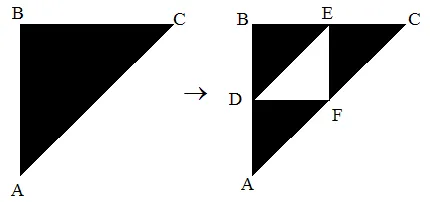
बिंदुओं के निर्देशांक हैं:

  • A (0,0)
  • B (0,1)
  • C (1,1)
  • D(0,1/2)
  • E (1/2,1)
  • F(1/2,1/2)

हमारे पास 3 ट्रांसफॉर्मेशन हैं:

  1. ABC -> ADF
  2. ABC -> DBE
  3. ABC -> FEC

रैखिक समीकरणों की प्रणाली इस प्रकार है:




हल हैं: , ,

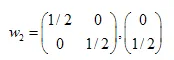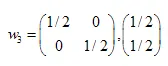
हमने तीन एफ़ाइन ट्रांसफॉर्म के गुणांक खोज लिए हैं। आगे हम उनका उपयोग आत्म-समरूप सेट बनाने के लिए करेंगे।


3. Iterated Function Systems का उपयोग कर फ्रैक्टल बनाना

Iterated Function System (IFS) एफ़ाइन संकुचन का एक सेट 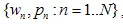है जहां 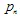- "वजन" है। प्रत्येक IFS फ़ंक्शन 7 संख्याओं द्वारा परिभाषित किया जाता है: 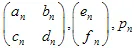, जहां 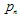वजन का उपयोग इटरशन प्रक्रिया में n-थ ट्रांसफॉर्मेशन की संभावना के रूप में किया जाता है। बेहतर होगा कि उनके मानों को संकुचन के अनुपात के अनुसार परिभाषित किया जाए: ।

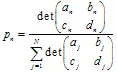आइए Iterated Function System का उपयोग करके फ्रैक्टल निर्माण के एल्गोरिदम पर विचार करें (देखें Chaos Game)।

पहले हमें कुछ प्रारंभिक बिंदु के साथ 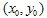लेना है। अगले, हम संयोग से कुछ संकुचन चुनते हैं और बिंदु 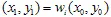को प्लॉट करते हैं। और फिर, एक बार फिर, चलो संयोग से एक संकुचन चुनते हैं 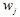और 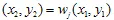को प्लॉट करते हैं। अंततः हमारे पास 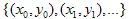के रूप में बिंदुओं का एक सेट होगा।

संकुचन का चयन इसके "संभाव्यता" पर निर्भर करता है। यदि हम प्रक्रिया को दोहराते हैं (उदाहरण के लिए, ~30000 बिंदुओं के लिए) और परिणामी सेट को प्लॉट करते हैं, तो हम इसकी संरचना देखेंगे भले ही यह प्रक्रिया यादृच्छिक हो।

यहाँ Sierpinski Gasket का एक उदाहरण है:

चित्र 1. Sierpinski Gasket, जो IFS गुणांक के साथ उत्पन्न हुआ

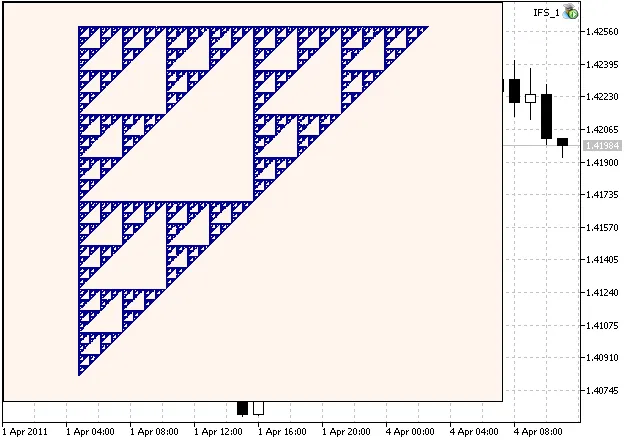
चित्र 1. Sierpinski Gasket, जो IFS गुणांक के साथ उत्पन्न हुआ

कोड:

//+------------------------------------------------------------------+
//|                                        IFS_Sierpinski_Gasket.mq5 |
//|                        Copyright 2011, MetaQuotes Software Corp. |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2011, MetaQuotes Software Corp."
#property link      "https://www.mql5.com"
#property version   "1.00"

//-- cIntBMP वर्ग के साथ शामिल करें
#include <cIntBMP.mqh>

//-- सिरपिंस्की गास्केट IFS गुणांक
//-- (a,b,c,d) मैट्रिक्स
double IFS_a[3] = {0.50,  0.50,  0.50};
double IFS_b[3] = {0.00,  0.00,  0.00};
double IFS_c[3] = {0.00,  0.00,  0.00};
double IFS_d[3] = {0.50,  0.50,  0.50};
//-- (e,f) वेक्टर
double IFS_e[3] = {0.00,  0.00,  0.50};
double IFS_f[3] = {0.00,  0.50,  0.50};
//-- ट्रांसफॉर्म की "संभावनाएं", 1000 से गुणा की गईं
double IFS_p[3]={333,333,333};

double Probs[3]; // Probs array - IFS ट्रांसफॉर्म चुनने के लिए उपयोग किया जाता है
cIntBMP bmp;     // cIntBMP वर्ग का उदाहरण
int scale=350;  // स्केल गुणांक
//+------------------------------------------------------------------+
//| एक्सपर्ट प्रारंभिककरण कार्य                                                |
//+------------------------------------------------------------------+
int OnInit()
  {
//-- Probs array तैयार करें
   double m=0;
   for(int i=0; i<ArraySize(IFS_p); i++)
     {
      Probs[i]=IFS_p[i]+m;
      m=m+IFS_p[i];
     }
//-- BMP इमेज का आकार
   int XSize=500;
   int YSize=400;
//-- clrSeashell बैकग्राउंड रंग के साथ XSizexYSize के साथ bmp इमेज बनाएं
   bmp.Create(XSize,YSize,clrSeashell);
//-- इमेज आयत
   bmp.DrawRectangle(0,0,XSize-1,YSize-1,clrBlack);

//-- बिंदुओं के निर्देशांक (सेट के निर्माण में उपयोग किया जाएगा)
   double x0=0;
   double y0=0;
   double x,y;
//-- गणना करने के लिए बिंदुओं की संख्या (अधिक बिंदु - विस्तृत इमेज)
   int points=1500000;
//-- सेट की गणना करें
   for(int i=0; i<points; i++)
     {
      // संभावनाओं के अनुसार IFS ट्रांसफॉर्म चुनें, परिभाषित
      double prb=1000*(rand()/32767.0);
      for(int k=0; k<ArraySize(IFS_p); k++)
        {
         if(prb<=Probs[k])
           {
            // एफ़ाइन ट्रांसफॉर्मेशन
            x = IFS_a[k] * x0 + IFS_b[k] * y0 + IFS_e[k];
            y = IFS_c[k] * x0 + IFS_d[k] * y0 + IFS_f[k];
            // पिछले निर्देशांक को अपडेट करें
            x0 = x;
            y0 = y;
            // BMP इमेज निर्देशांक में परिवर्तित करें
            // (cIntBMP में Y धुरी पर ध्यान दें)
            int scX = int (MathRound(XSize/2 + (x-0.5)*scale));
            int scY = int (MathRound(YSize/2 + (y-0.5)*scale));
            // यदि बिंदु के निर्देशांक इमेज में हैं, तो बिंदु खींचें
            if(scX>=0 && scX<XSize && scY>=0 && scY<YSize) { bmp.DrawDot(scX,scY,clrDarkBlue); }
            break;
           }
        }
     }
//-- इमेज को फ़ाइल में सहेजें
   bmp.Save("bmpimg",true);
//-- चार्ट पर इमेज प्लॉट करें
   bmp.Show(0,0,"bmpimg","IFS");
//---
   return(0);
  }
//+------------------------------------------------------------------+
//| एक्सपर्ट डीनिशियलाइजेशन कार्य                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//--- चार्ट से इमेज हटाएं
   ObjectDelete(0,"IFS");
//--- फ़ाइल हटाएं
   bmp.Delete("bmpimg",true);
  }
//+------------------------------------------------------------------+

यदि हम स्केल को 1350 पर सेट करते हैं, पुनरावृत्तियों की संख्या को 15000000 बढ़ाते हैं और प्रारंभिक बिंदु को स्थानांतरित करते हैं:

int scX = MathRound(XSize/2 + (x-0.75)*scale);
int scY = MathRound(YSize/2 + (y-0.75)*scale);

हम सेट का ज़ूम किए गए क्षेत्र देखेंगे। कोई देख सकता है (चित्र 2), कि इसकी आत्म-समरूप संरचना है:

चित्र 2. Sierpinski Gasket का ज़ूम किया हुआ क्षेत्र

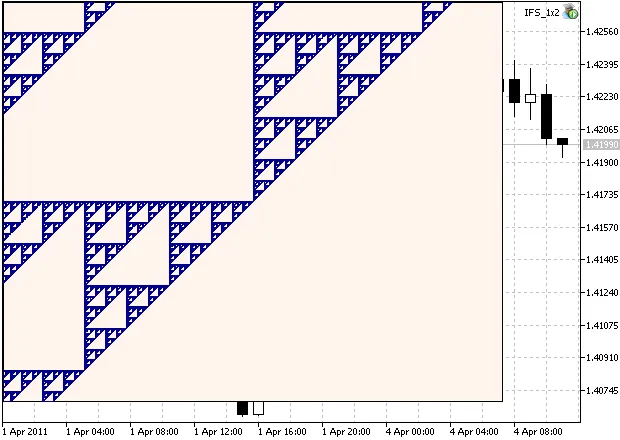
चित्र 2. Sierpinski Gasket का ज़ूम किया हुआ क्षेत्र

आइए प्रसिद्ध Barnsley's Fern पर विचार करें, जिसे Michael Barnsley द्वारा प्रस्तावित किया गया था। यह अधिक जटिल है।

चित्र 3. Barnsley's Fern

चित्र 3. Barnsley's Fern

कोड समान है, लेकिन इस मामले में हमारे पास अलग वजन के साथ 4 IFS संकुचन हैं।

//+------------------------------------------------------------------+
//|                                                     IFS_fern.mq5 |
//|                        Copyright 2011, MetaQuotes Software Corp. |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2011, MetaQuotes Software Corp."
#property link      "https://www.mql5.com"
#property version   "1.00"
#include <cIntBMP.mqh>
//-- Barnsley Fern IFS गुणांक
//-- (a,b,c,d) मैट्रिक्स
double IFS_a[4] = {0.00,  0.85,  0.20,  -0.15};
double IFS_b[4] = {0.00,  0.04, -0.26,   0.28};
double IFS_c[4] = {0.00, -0.04,  0.23,   0.26};
double IFS_d[4] = {0.16,  0.85,  0.22,   0.24};
//-- (e,f) वेक्टर
double IFS_e[4] = {0.00,  0.00,  0.00,   0.00};
double IFS_f[4] = {0.00,  1.60,  1.60,   0.00};
//-- ट्रांसफॉर्म की "संभावनाएं", 1000 से गुणा की गईं
double IFS_p[4] = {10,     850,    70,     70};

double Probs[4];
cIntBMP bmp;
int scale=50;
//+------------------------------------------------------------------+
//| एक्सपर्ट प्रारंभिककरण कार्य                                    |
//+------------------------------------------------------------------+
int OnInit()
  {
   double m=0;
   for(int i=0; i<ArraySize(IFS_p); i++)
     {
      Probs[i]=IFS_p[i]+m;
      m=m+IFS_p[i];
     }

   int XSize=600;
   int YSize=600;

   bmp.Create(XSize,YSize,clrSeashell);

   bmp.DrawRectangle(0,0,XSize-1,YSize-1,clrBlack);

   double x0=0;
   double y0=0;
   double x,y;

   int points=250000;

   for(int i=0; i<points; i++)
     {
      double prb=1000*(rand()/32767.0);
      for(int k=0; k<ArraySize(IFS_p); k++)
        {
         if(prb<=Probs[k])
           {
            x = IFS_a[k] * x0 + IFS_b[k] * y0 + IFS_e[k];
            y = IFS_c[k] * x0 + IFS_d[k] * y0 + IFS_f[k];
            x0 = x;
            y0 = y;
            int scX = int (MathRound(XSize/2 + (x)*scale));
            int scY = int (MathRound(YSize/2 + (y-5)*scale));
            if(scX>=0 && scX<XSize && scY>=0 && scY<YSize) { bmp.DrawDot(scX,scY,clrForestGreen); }
            break;
         }
    }
  }
   bmp.Save("bmpimg",true);
   bmp.Show(0,0,"bmpimg","Fern");
//---
   return(0);
  }
//+------------------------------------------------------------------+
//| एक्सपर्ट डीनिशियलाइजेशन कार्य                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int r)
  {
   //-- ग्रिड मोड को पुनर्स्थापित करें
   ChartSetInteger(0,CHART_SHOW_GRID,gridmode); 
//-- फ़र्न ऑब्जेक्ट हटाएं
   ObjectDelete(0,"Fern");
 }
//+------------------------------------------------------------------+
//| एक्सपर्ट OnChart इवेंट हैंडलर                                     |
//+------------------------------------------------------------------+
void OnChartEvent(const int id,           // इवेंट पहचानकर्ता  
                const long& lparam,   // लंबाई प्रकार का इवेंट पैरामीटर
                const double& dparam, // डबल प्रकार का इवेंट पैरामीटर
                const string& sparam  // स्ट्रिंग प्रकार का इवेंट पैरामीटर
                )
  {
//--- ग्राफिकल ऑब्जेक्ट पर क्लिक करें
   if(id==CHARTEVENT_OBJECT_CLICK)
     {
      Print("ग्राफिकल ऑब्जेक्ट पर क्लिक इवेंट नाम '                        
संबंधित पोस्ट
सूची
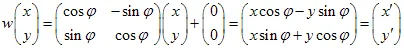
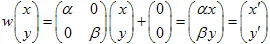
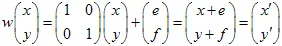
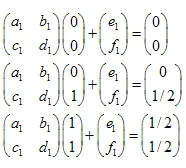
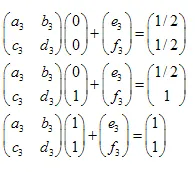
टिप्पणी (0)