はじめに
フラクタルを生成するソフトは数多くありますが、特にイテレーティッドファンクションシステム (IFS)を利用したものが注目されています。例えば、Fractintやフラクタルデザイナー、またはIFS Matlab Generatorなどがその例です。
MQL5言語のスピードとグラフィックオブジェクトとの相性の良さにより、これらの美しいフラクタルをMetaTrader 5のクライアント端末で簡単に研究することができます。
ここでは、cIntBMPライブラリを活用し、フラクタルの生成方法について具体的な例を見ていきます。このライブラリは、グラフィック画像の作成を大幅に簡素化し、特別賞を受賞した実績があります。
以下では、イテレーティッドファンクションシステムを用いたフラクタルの生成アルゴリズムを詳しく解説します。
1. 平面のアフィン変換
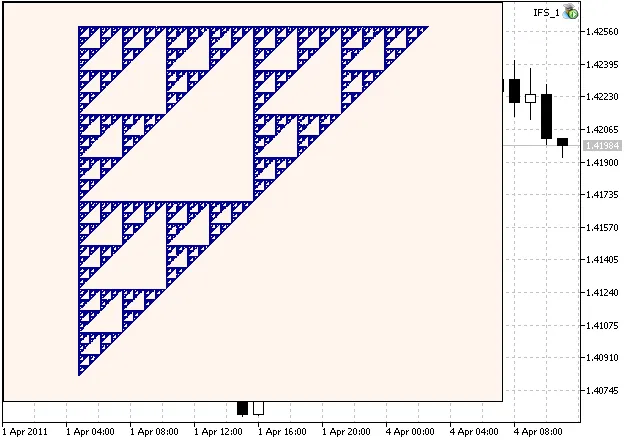
アフィン変換は、平面のマッピングを行います。一般的に、アフィン2D変換は、行列とベクトルを用いて定義され、座標(x,y)の点は線形変換により他の点に変換されます。
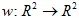
この変換は非特異でなければならず、アフィン変換はオブジェクトの幾何学的構造を変えることなく、単純な「変形」を記述することが可能です。
以下はアフィン平面変換の例です:
1) 平面の回転:2) 平面のスケーリング:
3) 平面の平行移動:
アフィン変換は、フラクタルの構造において重要な役割を果たします。次に、フラクタル集合を生成するためのアルゴリズムについて見ていきましょう。
2. 類似性変換
フラクタルは、ある幾何学的オブジェクトをN個の部分に分割し、そのうちM個を利用して集合の「構築」を行うことによって生成されます。このプロセスは繰り返され、フラクタルの自己相似構造が形成されます。
クラシックなフラクタルの例としては、以下のようなものがあります:
- トライアディックコッホ曲線 (N=3, M=4);
- カントールダスト (N=3, M=2);
- シェルピンスキーの三角形 (N=4, M=3);
- シェルピンスキーのカーペット (N=9, M=8);
フラクタルは自己相似の構造を持ち、いくつかの類似変換によって定義されることができます。次に、フラクタルの構築アルゴリズムを見ていきましょう。
3. IFSを用いたフラクタルの生成
イテレーティッドファンクションシステム(IFS)は、アフィン収縮の集合として定義されます。各IFS関数は、7つの数値で定義され、反復プロセス中のn番目の変換の確率として重みが使用されます。
フラクタル構築のアルゴリズムを考えてみましょう。最初に、初期点を選び、そこからランダムに収縮を選択します。このプロセスを繰り返すことで、最終的なフラクタル構造を得ることができます。
以上が、イテレーティッドファンクションシステムを用いたフラクタルの生成に関する基本的な説明です。続いて、具体的なコーディングや実装方法についても触れていきます。
まとめ
今回は、イテレーティッドファンクションシステムを用いたフラクタルの生成方法について詳しく解説しました。また、cIntBMPライブラリを活用することで、グラフィック画像の処理が非常に簡単になることもご紹介しました。今後、より美しいフラクタルを生成するためのクラスを作成し、機能を追加することが楽しみですね!
フラクタルの構築には、確率に基づいた正確な構造が求められます。確率の違いは、フラクタルの不規則な構造を生み出す要因となります。この特性を利用して、美しい画像を作成することができるのです。

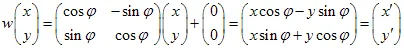
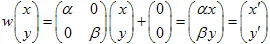
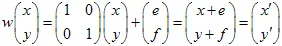
コメント 0