프랙탈 적응 이동 평균(FrAMA)는 존 엘러스(John Ehlers)가 개발한 기술적 지표입니다.
이 지표는 지수 이동 평균(EMA) 알고리즘을 기반으로 하여, 가격 시리즈의 현재 프랙탈 차원에 따라 스무딩 계수를 계산합니다. FrAMA의 장점은 강한 추세를 잘 따르면서 가격이 통합될 때 적절히 느려질 수 있다는 점입니다.
모든 유형의 이동 평균 분석 기법이 이 지표에 적용될 수 있습니다.
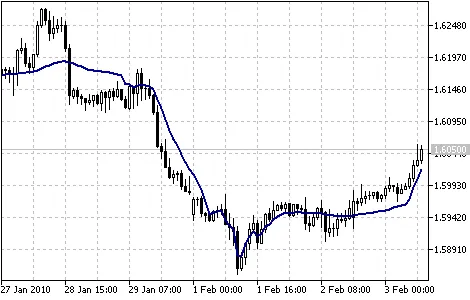
프랙탈 적응 이동 평균 지표
계산:
FRAMA(i) = A(i) * Price(i) + (1 - A(i)) * FRAMA(i-1)
여기서:
- FRAMA(i) - 현재 FrAMA 값;
- Price(i) - 현재 가격;
- FRAMA(i-1) - 이전 FrAMA 값;
- A(i) - 현재 지수 스무딩 계수.
지수 스무딩 계수는 아래 공식을 통해 계산됩니다:
A(i) = EXP(-4.6 * (D(i) - 1))
여기서:
- D(i) - 현재 프랙탈 차원;
- EXP() - 지수 함수.
직선의 프랙탈 차원은 1입니다. 공식에서 D = 1일 때, A = EXP(-4.6 * (1-1)) = EXP(0) = 1이 됩니다. 따라서 가격이 직선으로 변화할 때는 지수 스무딩이 사용되지 않으며, 공식은 다음과 같습니다:
FRAMA(i) = 1 * Price(i) + (1 - i) * FRAMA(i-1) = Price(i)
즉, 이 지표는 가격을 정확히 따릅니다.
평면의 프랙탈 차원은 2입니다. 공식을 통해 D = 2일 때, 스무딩 계수 A = EXP(-4.6*(2-1)) = EXP(-4.6) = 0.01이 됩니다. 이렇게 작은 값의 지수 스무딩 계수는 가격이 강한 톱니바퀴 형태로 움직일 때 발생합니다. 이러한 강한 느림은 약 200기간 단순 이동 평균에 해당합니다.
프랙탈 차원의 공식:
D = (LOG(N1 + N2) - LOG(N3))/LOG(2)
추가 공식에 따라 계산됩니다:
N(Length,i) = (HighestPrice(i) - LowestPrice(i))/Length
여기서:
- HighestPrice(i) - Length 기간의 현재 최대값;
- LowestPrice(i) - Length 기간의 현재 최소값;
N1, N2 및 N3 값은 각각:
N1(i) = N(Length,i)
N2(i) = N(Length,i + Length)
N3(i) = N(2 * Length,i)
