안녕하세요, 트레이더 여러분! 오늘은 부드러운 ADX(Smoothed ADX) 지표에 대해 이야기해볼까 해요. 이 지표는 포럼 방문자의 요청으로 만들어졌고, 실제로 구현하는 것은 그리 어렵지 않았습니다. 하지만 부드러운 ADX 알고리즘에 대한 설명은 찾기 힘들었어요. 그래서 이번 포스팅에서는 코드와 함께 간단한 설명을 드릴게요!
부드러운 ADX 코드
먼저, 다음은 부드러운 ADX 지표의 코드입니다:
Inputs: {입력값 선언}
Length(14),
ADXTrend(25), alpha1(0.25), alpha2(0.33);
Length(14),
ADXTrend(25), alpha1(0.25), alpha2(0.33);
variables: {변수 선언}
DMIPlus(0), DMIMinus(0), DMI(0), ADX(0),
DIPlusLead(0), DIMinusLead(0), DIPlusFinal(0), DIMinusFinal(0),
ADXLead(0), ADXFinal(0);
DMIPlus(0), DMIMinus(0), DMI(0), ADX(0),
DIPlusLead(0), DIMinusLead(0), DIPlusFinal(0), DIMinusFinal(0),
ADXLead(0), ADXFinal(0);
{ADX의 내장 함수 호출, 그래서 직접 계산할 필요 없음}
Value1 = DirMovement(H, L, C, Length, DMIPlus, DMIMinus, ADX);
부드러운 ADX 지표의 실제 스무딩 부분
DIPlusLead = 2*DMIPlus + (alpha1 - 2) * DMIPlus[1] + (1 - alpha1) * DIPlusLead[1];
DIPlusFinal = alpha2*DIPlusLead + (1 - alpha2) * DIPlusFinal[1];
DIPlusLead = 2*DMIPlus + (alpha1 - 2) * DMIPlus[1] + (1 - alpha1) * DIPlusLead[1];
DIPlusFinal = alpha2*DIPlusLead + (1 - alpha2) * DIPlusFinal[1];
DIMinusLead = 2*DMIMinus + (alpha1 - 2) * DMIMinus[1] + (1 - alpha1) * DIMinusLead[1];
DIMinusFinal = alpha2*DIMinusLead + (1 - alpha2) * DIMinusFinal[1];
DIMinusFinal = alpha2*DIMinusLead + (1 - alpha2) * DIMinusFinal[1];
ADXLead = 2*ADX + (alpha1 - 2) * ADX[1] + (1 - alpha1) * ADXLead[1];
ADXFinal = alpha2*ADXLead + (1 - alpha2) * ADXFinal[1];
ADXFinal = alpha2*ADXLead + (1 - alpha2) * ADXFinal[1];
{차트에 플로팅하기}
Plot1(DIPlusFinal, "DMI+");
Plot2(DIMinusFinal, "DMI-");
Plot3(ADXFinal, "ADX");
Plot2(DIMinusFinal, "DMI-");
Plot3(ADXFinal, "ADX");
부드러운 ADX의 스무딩 과정
부드러운 ADX의 초기 텍스트에 깊이 들어가지 않으면, 이 스무딩은 두 단계로 나눌 수 있어요. 예를 들어, 우리가 P라는 숫자 시퀀스가 있다고 가정하고, 최소한의 지연으로 스무딩을 해야 한다고 해봅시다. 첫 번째 단계에서는 다음 공식을 사용하여 P-시퀀스의 진동 함수 V(P)를 구축합니다:
- P0는 시퀀스의 현재 값(가격 또는 지표);
- P1은 시퀀스의 이전 값;
- V1은 이전 진동 값;
- V0는 현재 진동 값입니다.
또는 다른 방식으로:
V0 = (Vol(P) + 3*V1) / 4,
여기서:
Vol(P) = 8*P0 - 7*P1 - Ehlers의 폭발(제가 만든 용어입니다).
두 번째 단계에서는 간단한 가중치 스무딩을 적용합니다:
W0 = (1*V0 + 2*W1) / (2 + 1).
여기서:
- W0는 시퀀스 P의 현재 스무딩 값;
- V0는 P-시퀀스의 현재 진동 값;
- W1은 이전 스무딩 값입니다.
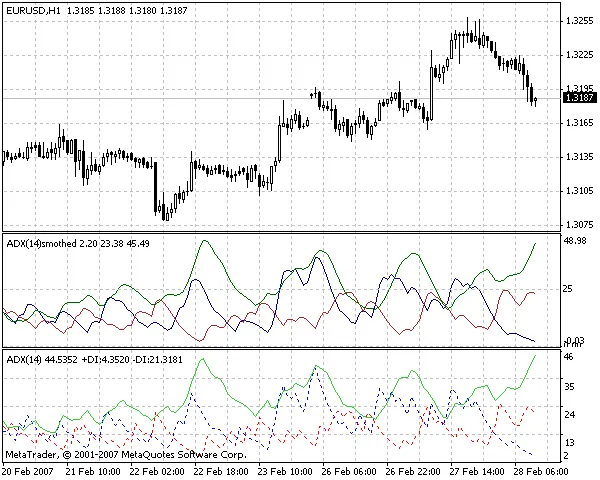
부드러운 ADX에서는 이 스무딩 알고리즘이 표준 ADX의 모든 세 가지 버퍼에 적용됩니다. 그래서 이 지표는 부드러운 ADX라고 불리는 것이죠. 만약 RSI 지표를 스무딩한다면, 그걸 부드러운 RSI라고 부르겠죠. 아래 그림은 부드러운 ADX가 실제로 원래의 표준 ADX(평균 방향성 이동 지수)보다 덜 '떨리는' 모습을 보여줍니다.