가격 시리즈 x[i] (i=1..n)의 다중 조화(혹은 다중 톤) 삼각 함수 모델은 다음과 같이 표현됩니다:
x[i] = m + Σ(a[h]*Cos(w[h]*i) + b[h]*Sin(w[h]*i), h=1..H)
여기서:
- x[i] - i번째 바의 과거 가격, 총 n개의 과거 가격;
- m - 바이어스;
- a[h]와 b[h] - 조화의 스케일링 계수;
- w[h] - 조화의 주파수;
- h - 조화 번호;
- H - 적합된 조화의 총 개수.
이 모델을 적합시키는 것은 실제 값에 가까운 m, a[h], b[h], w[h]를 찾는 것을 의미합니다. 조화 주파수 w[h]를 찾는 것이 삼각 함수 모델을 적합시키는 가장 어려운 부분입니다. 푸리에 급수의 경우, 이 주파수는 2πh/n으로 설정됩니다. 하지만, 푸리에 외삽은 단순히 n개의 과거 가격을 미래로 반복하는 것에 불과합니다.
이 지표는 Quinn-Fernandes 알고리즘을 사용하여 조화 주파수를 찾습니다. 지정된 총 조화 개수 H에 도달할 때까지 삼각 함수 시리즈의 조화를 하나씩 적합합니다. 새로운 조화를 적합한 후, 코딩된 알고리즘은 업데이트된 모델과 실제 값 간의 잔차를 계산하고 잔차에 새로운 조화를 적합합니다.
이 지표는 다음과 같은 입력 매개변수를 가집니다:
- Npast - 삼각 함수 시리즈가 적합되는 과거 바의 수;
- Nfut - 예측되는 미래 바의 수;
- Nharm - 모델의 총 조화 개수;
- FreqTOL - 주파수 계산의 허용 오차.
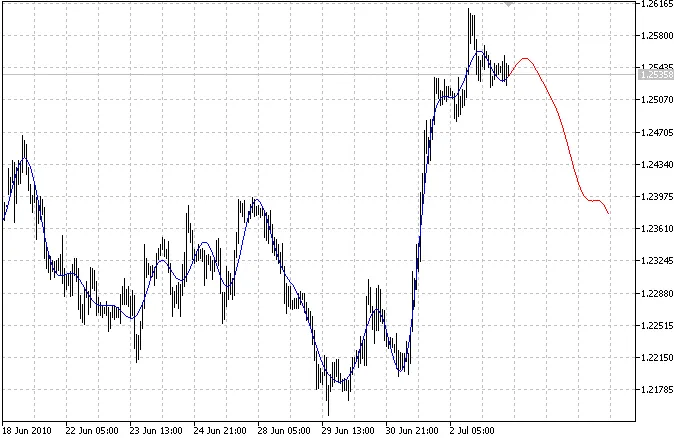
이 지표는 두 개의 곡선을 플로팅합니다: 파란 곡선은 모델링된 과거 값을, 빨간 곡선은 모델링된 미래 값을 나타냅니다.