作者:安德烈·N·博尔康斯基
Stochastic Momentum(随机动量指标,简称 SM)由威廉·布劳(William Blau)提出,详见他的著作 《动量、方向与背离:最新动量指标在技术分析中的应用》。
q周期的随机动量定义为当前收盘价与q根K线中点之间的距离。
- 随机动量的数值 表示q周期价格区间中点与当前价格之间的距离。
- 随机动量的符号 表示价格相对于价格区间中点的位置:当价格高于中点时为正值,低于中点时为负值。
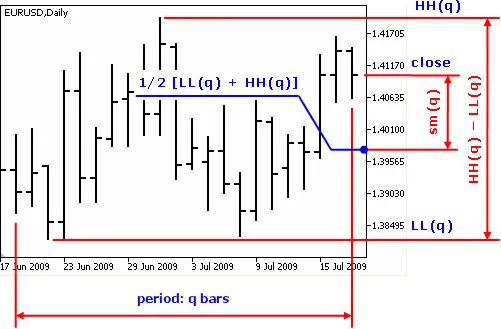
威廉·布劳的随机动量定义
- WilliamBlau.mqh 文件必须放置在 terminal_data_folder\MQL5\Include\
- Blau_SM.mq5 文件必须放置在 terminal_data_folder\MQL5\Indicators\
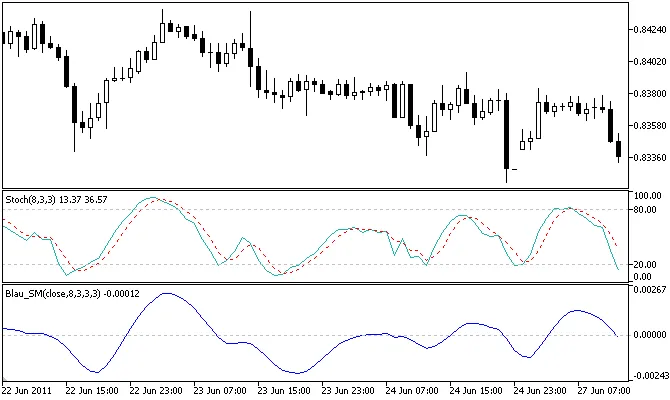
计算公式:
q周期随机动量的计算公式如下:
sm(price,q) = price - 1/2 * [LL(q) + HH(q)]
其中:
- price - 收盘价;
- q - 用于计算随机动量的K线数量;
- LL(q) - 最低价(q根K线);
- HH(q) - 最高价(q根K线);
- 1/2*[LL(q)+HH(q)] - q周期价格区间的中点。
平滑的q周期随机动量计算公式为:
SM(price,q,r,s,u) = EMA(EMA(EMA(sm(price,q),r),s),u)
其中:
- price - 收盘价;
- q - 用于计算随机动量的K线数量;
- sm(price,q)=price-1/2*[LL(q)+HH(q)] - q周期随机动量;
- EMA(sm(price,q),r) - 第一次平滑 - 指数平滑移动平均,周期为r,应用于q周期随机动量;
- EMA(EMA(...,r),s) - 第二次平滑 - 应用在第一次平滑结果上的EMA,周期为s;
- EMA(EMA(EMA(sm(q),r),s),u) - 第三次平滑 - 应用在第二次平滑结果上的EMA,周期为u。
- q - 随机动量的周期(默认q=5);
- r - 应用于随机动量的第一次EMA周期(默认r=20);
- s - 应用于第一次平滑结果的第二次EMA周期(默认s=5);
- u - 应用于第二次平滑结果的第三次EMA周期(默认u=3);
- AppliedPrice - 价格类型(默认AppliedPrice=PRICE_CLOSE)。
- q>0;
- r>0, s>0, u>0。如果r、s或u=1,则不使用平滑;
- 最小率=(q-1+r+s+u-3+1)。
