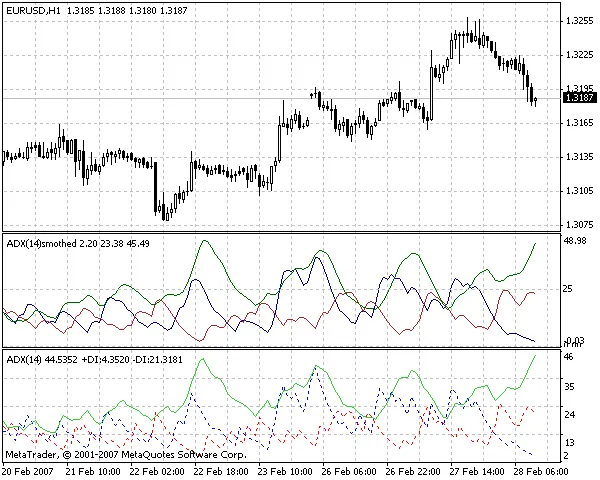
大家好,今天我们来聊聊平滑ADX指标,这个指标是应某位论坛朋友的要求而编写的,实际上也不算太复杂。不过,关于平滑ADX算法的描述在网上几乎没有找到,因此我将直接分享代码。
输入参数:
长度(14),
ADX趋势(25), alpha1(0.25), alpha2(0.33);
变量:
DMI正(0), DMI负(0), DMI(0), ADX(0),
DMI正引导(0), DMI负引导(0), DMI正最终(0), DMI负最终(0),
ADX引导(0), ADX最终(0);
接下来,我们调用内置的ADX函数,这样就不需要自己计算了:
接下来是对原始ADX指标进行平滑处理,DI+、DI-和ADX线都将被平滑:
DI正引导 = 2*DMI正 + (alpha1 - 2) * DMI正[1] + (1 - alpha1) * DMI正引导[1];DI正最终 = alpha2*DI正引导 + (1 - alpha2) * DMI正最终[1];
DI负最终 = alpha2*DI负引导 + (1 - alpha2) * DMI负最终[1];
ADX最终 = alpha2*ADX引导 + (1 - alpha2) * ADX最终[1];
最后,我们将在图表上绘制这些线:
Plot1(DI正最终, "DMI+");
Plot2(DI负最终, "DMI-");
Plot3(ADX最终, "ADX");
实际上,如果你不深入理解平滑ADX背后的深层含义,这个平滑过程可以分为两个阶段。假设我们有一个数值序列P,需要以最小滞后进行平滑。我们在第一阶段构建函数V(P)来表示P序列的振荡,公式如下:
- P0是当前序列的值(价格或指标);
- P1是前一个序列的值;
- V1是前一个振荡值;
- V0是当前振荡值。
另一种表达方式是:
V0 = (Vol(P) + 3*V1) / 4,
其中:
Vol(P) = 8*P0 - 7*P1 - Ehlers的爆发(这个术语是我自己创造的)。
在第二阶段,我们应用简单的加权平滑:
W0 = (1*V0 + 2*W1) / (2 + 1)。
其中:
- W0是序列P的当前平滑值;
- V0是当前的P序列振荡值;
- W1是前一个平滑值。
在平滑ADX中,这个平滑算法被应用于标准ADX指标的所有三个缓冲区。这就是为什么我们称它为平滑ADX。如果我们对RSI指标进行平滑,我们就称之为平滑RSI等等。下面的图表显示,平滑ADX确实不像原始的标准ADX(平均方向运动指数)那样“剧烈”。