在当今的金融市场中,分形时间函数的代表性应用主要体现在金融时间序列上。这些时间序列的分形结构众所周知,正如曼德布罗特所言,市场的一个著名说法是:股票和货币的运动独立于时间尺度和价格。观察者仅凭图表的外观,无法判断信息是指周、日还是小时的变化。
通常,为了确定分形维数,我们会计算赫斯特指数。然而,可靠计算该指数需要大量的数据(约10^3),这与交易趋势的持续时间相比显得过于庞大。
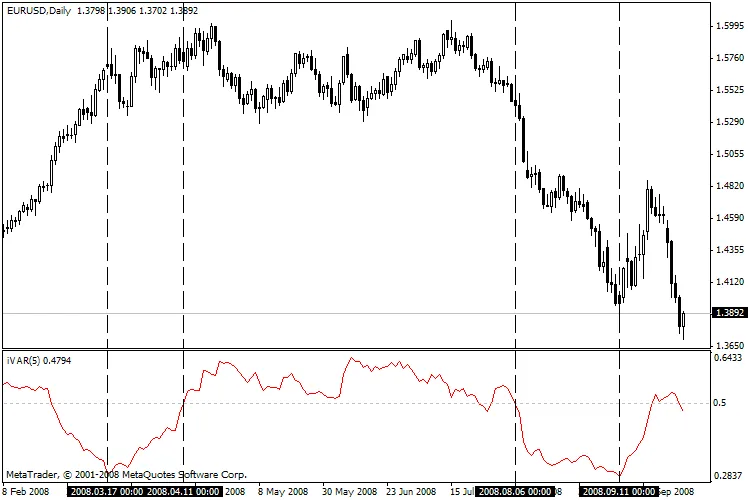
因此,作者们提出了一种变异指数(m),它与常见的分形维度密切相关。与赫斯特指数不同,确定该指数所需的信息量减少了2倍,因此可以作为局部特征来判断价格序列的动态变化。如果m < 0.5,这可以解读为趋势;如果m > 0.5,则可以视为震荡行情。
该指标计算的是前一个区间的变异指数,区间长度为2^n,用户可自行设定参数n。
使用该指标的一般规则如下:
- 如果指标值低于0.5,表示市场处于趋势状态。
- 极低的值通常预示当前趋势的结束(调整)。
- 如果指标值高于0.5,表示市场处于震荡状态。
- 极高的值往往预示着重大趋势的开始。
- 如果指标值接近0.5,表示市场状态不明确。
参考文献:
1. M.M. Dubovikov等,《最小覆盖维数与分形时间序列的局部分析》,2004年。
2. Edgar E. Peters,《分形市场分析:将混沌理论应用于投资和经济学》,约翰·威利父子公司,2003年。
