本物の著者:
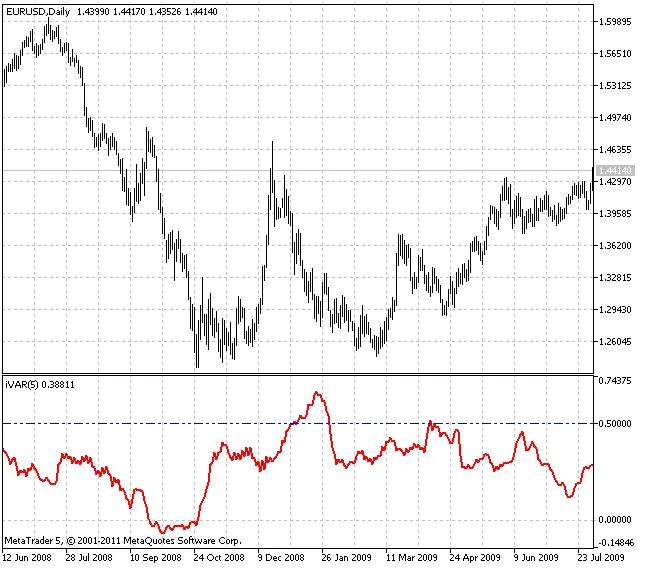
バリエーションインデックスは、時系列においてトレンドまたはフラットな動きが支配しているか、もしくはランダムな行動が見られるかを示します。
現在、フラクタル時間関数の中で最も人気のある代表は金融時系列です。これらの時系列のフラクタル構造は広く知られており、マンデルブロは「市場のフォークロアの現実的な再定義、すなわち、株式や通貨の動きは、マーケットチャートが同じ時間および価格スケールに収まるように拡大または縮小されると、すべて似たような形になる」と述べています。
通常、フラクタル次元を決定するためにハースト指数が計算されます。しかし、この指数を信頼性高く計算するためには膨大なデータ(約1000件)が必要であり、それはトレンドの持続時間に比べて非常に多いです。
著者たちは、一般的なフラクタル次元と密接に関連するフラクタル特性としてバリエーションインデックス(m)を提案しています。ハースト指数とは異なり、インデックスの決定に必要な情報量は2倍少なくて済みます。これにより、価格シリーズのダイナミクスを決定するためのローカル特性として利用できるようになります。mが0.5未満であればトレンド、0.5を超えていればフラットと解釈できます。
提案されたインジケーターは、過去のインターバル(長さは2^n)に基づいてバリエーションインデックスを計算します。"n"パラメータはユーザーが指定します。
インジケーターの一般的な適用ルールは以下の通りです:
- インジケーターの値が0.5未満の場合、市場はトレンド状態です。
- 極端に低い値は、現在のトレンドの終わり(調整)を予告することが多いです。
- インジケーターの値が0.5を超える場合、市場はフラット状態です。
- 極端に高い値は、重要なトレンドの始まりを予告することが多いです。
- インジケーターの値が0.5に近い場合、市場の状態は不明瞭です。
このインジケーターは初めてMQL4で実装され、mql4.comのCodeBaseに2008年10月6日に公開されました。
参考文献
- M.M. Dubovikov et al, 最小被覆の次元とフラクタル時系列のローカル分析, 2004.
- Edgar E. Peters, フラクタル市場分析。投資と経済学へのカオス理論の応用, John Wiley & Sons, 2003.
