ค่าเฉลี่ยเคลื่อนที่แบบเอ็กซ์โปเนนเชียลสามเท่า (TEMA) เป็นเครื่องมือทางเทคนิคที่พัฒนาโดย Patrick Mulloy และถูกเผยแพร่ใน นิตยสาร "Technical Analysis of Stocks & Commodities"
หลักการในการคำนวณของ TEMA จะคล้ายกับ ค่าเฉลี่ยเคลื่อนที่แบบเอ็กซ์โปเนนเชียลสองเท่า (DEMA) ซึ่งชื่อ "Triple Exponential Moving Average" อาจไม่สะท้อนถึงอัลกอริธึมของมันได้อย่างถูกต้องนัก เพราะมันเป็นการรวมกันที่ไม่เหมือนใครของค่าเฉลี่ยเคลื่อนที่แบบเอ็กซ์โปเนนเชียลแบบเดี่ยว แบบคู่ และแบบสามเท่า ที่ให้การหน่วงเวลาน้อยกว่าทั้งสามแบบเมื่อใช้แยกกัน
TEMA สามารถใช้แทนค่าเฉลี่ยเคลื่อนที่แบบดั้งเดิมได้ โดยมันสามารถใช้เพื่อการเรียบเรียงข้อมูลราคาหรือแม้กระทั่งเรียบเรียงตัวชี้วัดอื่นๆ ได้
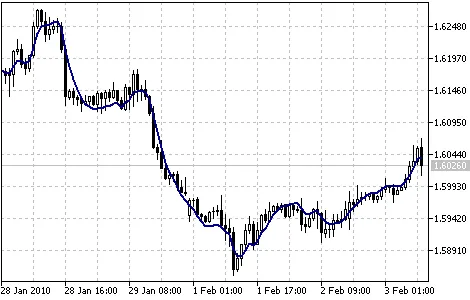
ค่าเฉลี่ยเคลื่อนที่แบบเอ็กซ์โปเนนเชียลสามเท่า
การคำนวณ:
เริ่มต้นจะคำนวณ DEMA ก่อน จากนั้นคำนวณความผันผวนของราคาจาก DEMA:
โดยที่:
- err(i) - ความผิดพลาดของ DEMA ในขณะนั้น;
- Price(i) - ราคาปัจจุบัน;
- DEMA(Price, N, i) - ค่า DEMA ปัจจุบันจากชุดข้อมูลราคาในช่วงเวลา N.
จากนั้นเพิ่มค่าของค่าเฉลี่ยเอ็กซ์โปเนนเชียลของความผิดพลาดและได้ TEMA:
= DEMA(Price, N, i) + EMA(Price - DEMA(Price, N, i), N, i) = 3 * EMA(Price, N, i) - 3 * EMA2(Price, N, i) + EMA3(Price, N, i)
โดยที่:
- EMA(err, N, i) - ค่าปัจจุบันของค่าเฉลี่ยเอ็กซ์โปเนนเชียลของความผิดพลาด err;
- EMA2(Price, N, i) - ค่าปัจจุบันของการเรียบเรียงราคาสองเท่า;
- EMA3(Price, N, i) - ค่าปัจจุบันของการเรียบเรียงราคาสามเท่า.
โพสต์ที่เกี่ยวข้อง
- AllAverages v4.9 MT5: เครื่องมือวิเคราะห์ที่นักเทรดต้องมี
- เครื่องมือ Open Range Breakout สำหรับ MetaTrader 5
- Multi_ATR_Bands: เครื่องมือการเทรดที่ต้องมีใน MetaTrader 5
- Tymen STARC Bands MTF: เครื่องมือวิเคราะห์หลายกรอบเวลาใน MetaTrader 5
- การวิเคราะห์สเปกตรัมเดี่ยว: ตัวชี้วัดแนวโน้มสำหรับ MetaTrader 5