การใช้แบบจำลองตรีโกณมิติมัลติฮาร์มอนิก (Multi-Harmonic) ในการวิเคราะห์ราคาสามารถช่วยให้เราทำนายแนวโน้มในตลาดได้อย่างมีประสิทธิภาพมากขึ้น โดยใช้ชุดข้อมูลราคาที่ผ่านมา x[i] ซึ่งหมายถึงราคาที่บาร์ที่ i ตั้งแต่ i=1 ถึง n ดังนี้:
x[i] = m + Sum( a[h]*Cos(w[h]*i) + b[h]*Sin(w[h]*i), h=1..H )
ในที่นี้:
- x[i] - ราคาที่ผ่านมา ณ บาร์ที่ i, จำนวนรวม n ราคาที่ผ่านมา;
- m - ค่าเบี่ยงเบน;
- a[h] และ b[h] - ค่าสเกลของฮาร์มอนิก;
- w[h] - ความถี่ของฮาร์มอนิก;
- h - หมายเลขฮาร์มอนิก;
- H - จำนวนฮาร์มอนิกทั้งหมดที่พอดี.
การปรับค่าต่างๆ ในโมเดลนี้หมายถึงการหาค่า m, a[h], b[h], และ w[h] ที่ทำให้ค่าที่ได้จากโมเดลใกล้เคียงกับค่าจริงมากที่สุด โดยการหาความถี่ของฮาร์มอนิก w[h] ถือเป็นส่วนที่ยากที่สุดในการปรับโมเดลตรีโกณมิติ สำหรับซีรีส์ฟูรีเยร์ ความถี่เหล่านี้จะถูกกำหนดที่ 2*pi*h/n แต่การคาดการณ์ด้วยซีรีส์ฟูรีเยร์นั้นหมายถึงการทำซ้ำราคาที่ผ่านมา n ไปยังอนาคต.
ตัวชี้วัดนี้ใช้ الگอริธึม Quinn-Fernandes ในการหาความถี่ของฮาร์มอนิก โดยจะปรับฮาร์มอนิกของซีรีส์ตรีโกณมิติทีละตัวจนกว่าจะถึงจำนวนฮาร์มอนิกทั้งหมดที่กำหนด H หลังจากการปรับฮาร์มอนิกใหม่แล้ว อัลกอริธึมจะคำนวณค่าความแตกต่างระหว่างโมเดลที่ปรับปรุงและค่าจริง และปรับฮาร์มอนิกใหม่ให้กับค่าความแตกต่างนั้น.
ตัวชี้วัดนี้มีพารามิเตอร์การป้อนข้อมูลดังนี้:
- Npast - จำนวนบาร์ที่ผ่านมา ที่จะปรับซีรีส์ตรีโกณมิติ;
- Nfut - จำนวนบาร์ในอนาคตที่คาดการณ์;
- Nharm - จำนวนฮาร์มอนิกทั้งหมดในโมเดล;
- FreqTOL - ความคลาดเคลื่อนในการคำนวณความถี่.
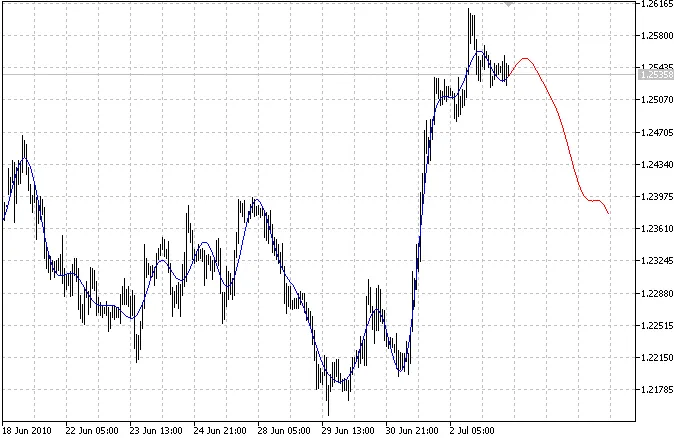
ตัวชี้วัดนี้จะแสดงเส้นกราฟสองเส้น: เส้นสีน้ำเงินจะแสดงค่าที่พอดีกับราคาที่ผ่านมา และเส้นสีแดงจะแสดงค่าที่พอดีกับราคาที่คาดการณ์ในอนาคต.
โพสต์ที่เกี่ยวข้อง
- เครื่องมือ Open Range Breakout สำหรับ MetaTrader 5
- เครื่องมือ Master Tools - อินดิเคเตอร์สำหรับ MetaTrader 4
- FX Multi-Meter II: เครื่องมือช่วยเทรดที่ครบครันสำหรับนักลงทุน
- ID Lite Info MA – ตัวช่วยวิเคราะห์ Moving Average สำหรับ MetaTrader 5
- Volume Profile + Range v6.0: เครื่องมือวิเคราะห์การซื้อขายใน MetaTrader 5
