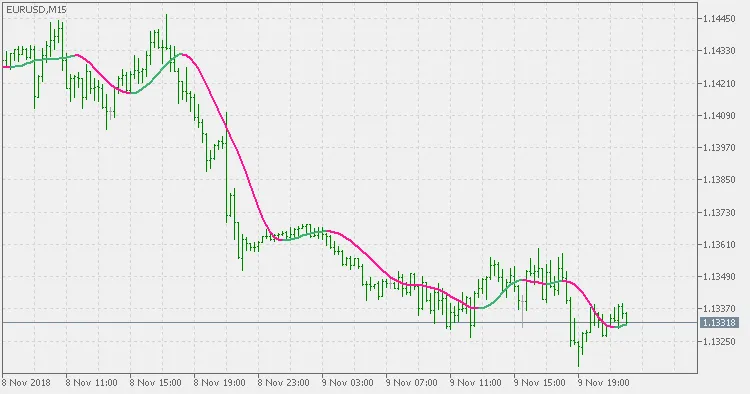
थ्योरी:
त्रिकोणीय मूविंग एवरेज एक प्रकार का वेटेड मूविंग एवरेज है, जो बहुत स्मूद परिणामों के लिए जाना जाता है। त्रिकोणीय मूविंग एवरेज में वेट्स मध्य मानों पर अधिक जोर देते हैं। इसी कारण, गुणांक विशेष रूप से वितरित होते हैं। यहाँ कुछ उदाहरण दिए गए हैं जो गुणांक के विकास को स्पष्ट रूप से दिखाते हैं:
पीरियड 1 : 1 पीरियड 2 : 1 1 पीरियड 3 : 1 2 1 पीरियड 4 : 1 2 2 1 पीरियड 5 : 1 2 3 2 1 पीरियड 6 : 1 2 3 3 2 1 पीरियड 7 : 1 2 3 4 3 2 1 पीरियड 8 : 1 2 3 4 4 3 2 1 पीरियड 9 : 1 2 3 4 5 4 3 2 1और ऐसे ही चलता रहेगा ...
त्रिकोणीय मूविंग एवरेज के कई कार्यान्वयन और परिभाषाएँ हैं। कुछ सटीक हैं और कुछ नहीं हैं (जो "सटीक नहीं" हैं, वे कभी नहीं समझ पाए कि आप विषम और सम पीरियड के लिए समान एवरेज मान नहीं रख सकते)। कुछ वास्तव में त्रिकोणीय मूविंग एवरेज की चर्चा का मजेदार व्याख्या हैं। सटीक विधियों में मुख्य रूप से केवल एक चीज की कमी है: वे बार-बार लूप होती हैं और लंबे पीरियड के लिए निष्पादन गति महत्वपूर्ण हो जाती है।
इस संस्करण:
निष्पादन गति को हल करता है जबकि सटीक परिणाम देता है (यहाँ विषम और सम पीरियड के लिए समान एवरेज मान नहीं हैं :))
उपयोग:
आप सिग्नल के रूप में रंग परिवर्तन का उपयोग कर सकते हैं। ध्यान दें कि, कई लोग जो केंद्रित TMA को TMA के साथ मिलाते हैं, यह केंद्रित TMA नहीं है और यह पुन: गणना या पुनः रंग नहीं करता है।