Autor original:
O Índice de Variação é um indicador que mostra se um movimento de tendência ou uma lateralização está predominando na série temporal, ou se o comportamento é aleatório.
Hoje em dia, os representantes mais populares das funções temporais fractais são as séries temporais financeiras. A estrutura fractal dessas séries é bem conhecida e, segundo Mandelbrot, é uma "reformulação teórica de um pedaço prático de folclore de mercado - ou seja, que os movimentos de uma ação ou moeda parecem semelhantes quando um gráfico de mercado é ampliado ou reduzido para caber na mesma escala de tempo e preço".
Normalmente, para determinar a dimensão fractal, calcula-se o expoente de Hurst. No entanto, para o cálculo confiável desse expoente, é necessário um grande volume de dados (~ 10^3), o que é excessivo considerando a duração das tendências de negociação.
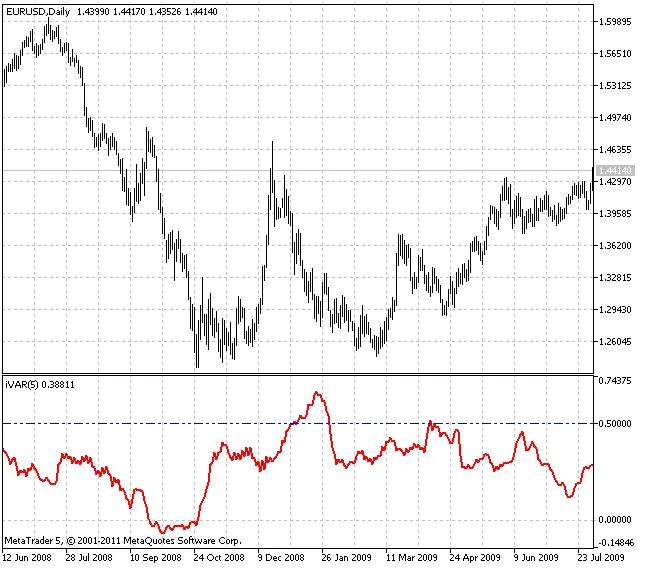
Os autores mencionados introduzem as características fractais - o índice de variação (m) que está intimamente relacionado à dimensão fractal comum. Ao contrário do expoente de Hurst, a quantidade de informação necessária para a determinação do índice é menor por um fator de 2. Isso permite seu uso como uma característica local para determinar a dinâmica das séries de preços. Se m < 0.5, pode ser interpretado como uma tendência e se m > 0.5 - como uma lateralização.
O indicador sugerido calcula o índice de variação em um intervalo anterior que é 2^n longo. O parâmetro "n" é especificado pelo usuário.
As regras gerais de aplicação do indicador são as seguintes:
- Se o valor do indicador for inferior a 0,5, significa que o mercado está em tendência.
- Um valor extremamente baixo geralmente precede o fim (correção) da tendência atual.
- Se o valor do indicador for superior a 0,5, significa que o mercado está lateralizado.
- Um valor extremamente alto frequentemente precede o início de tendências significativas.
- Se o valor do indicador estiver próximo de 0,5, significa que o estado do mercado é indefinido.
Esse indicador foi implementado pela primeira vez em MQL4 e publicado em CodeBase do mql4.com em 06.10.2008.
Referências
- M.M. Dubovikov et al, Dimensão da Cobertura Mínima e Análise Local de Séries Temporais Fractais, 2004.
- Edgar E. Peters, Análise de Mercado Fractal. Aplicando a Teoria do Caos a Investimentos e Economia, John Wiley & Sons, 2003.
Publicações relacionadas
- Calendário Econômico: Monitoramento e Cache para Testes de Estratégia no MetaTrader 5
- Buffers Horários para Coleta de Dados no MetaTrader 5
- Índice de Preferência do Investidor: Um Guia Prático para Traders
- Divergência no Awesome Oscillator: O Guia Completo para Traders
- Oscilador Maravilhoso e Divergências: Um Guia para MetaTrader 5
