Home Indicatore tecnico Post

Smoothed ADX: Guida all'Indicatore di Trading di John Ehlers

Mike • 2008-02-10 23:45
1 0 0
Allegato
7072.zip (1 KB, Scarica 0 volte)

Oggi parliamo dell'indicatore Smoothed ADX, un tool richiesto da un visitatore del forum e che si è rivelato non troppo complicato da implementare. Tuttavia, cercando informazioni sul funzionamento dell'algoritmo di smussamento dell'ADX, non ho trovato molto in giro. Ecco quindi un'analisi e il codice che ho preparato per voi!


Input:

  • Length(14)
  • ADXTrend(25)
  • alpha1(0.25)
  • alpha2(0.33)

Variabili:

  • DMIPlus(0)
  • DMIMinus(0)
  • DMI(0)
  • ADX(0)
  • DIPlusLead(0)
  • DIMinusLead(0)
  • DIPlusFinal(0)
  • DIMinusFinal(0)
  • ADXLead(0)
  • ADXFinal(0)

Iniziamo a calcolare i valori utilizzando le funzioni ADX integrate, così non dobbiamo calcolarli manualmente:

Value1 = DirMovement(H, L, C, Length, DMIPlus, DMIMinus, ADX);


Ora, passiamo alla parte di smussamento dell'indicatore ADX originale. Le linee DI+, DI- e ADX vengono smussate come segue:

DIPlusLead = 2*DMIPlus + (alpha1 - 2) * DMIPlus[1] + (1 - alpha1) * DIPlusLead[1];
DIPlusFinal = alpha2*DIPlusLead + (1 - alpha2) * DIPlusFinal[1];

DIMinusLead = 2*DMIMinus + (alpha1 - 2) * DMIMinus[1] + (1 - alpha1) * DIMinusLead[1];
DIMinusFinal = alpha2*DIMinusLead + (1 - alpha2) * DIMinusFinal[1];

ADXLead = 2*ADX + (alpha1 - 2) * ADX[1] + (1 - alpha1) * ADXLead[1];
ADXFinal = alpha2*ADXLead + (1 - alpha2) * ADXFinal[1];


Infine, andiamo a plottare i risultati sul grafico:

Plot1(DIPlusFinal, "DMI+");
Plot2(DIMinusFinal, "DMI-");
Plot3(ADXFinal, "ADX");


Se non vi addentrate nel significato profondo del testo iniziale dell'ADX smussato, potete considerare il processo di smussamento in due fasi. Immaginate di avere una sequenza numerica P e di doverla smussare con il minimo ritardo. Iniziamo costruendo la funzione V(P) dall'oscillazione della sequenza P usando questa formula:

  • V0 = (8*P0 - 7*P1 + 3*V1) / 4,

dove:

  • P0 è il valore attuale della sequenza (prezzo o indicatore);
  • P1 è il valore precedente della sequenza;
  • V1 è il valore precedente dell'oscillazione;
  • V0 è il valore attuale dell'oscillazione.

Oppure, in un altro modo:

  • V0 = (Vol(P) + 3*V1) / 4,

dove:

  • Vol(P) = 8*P0 - 7*P1 - l'esplosione di Ehlers (termine inventato da me).

Nella seconda fase, applicheremo uno smussamento pesato semplice:

  • W0 = (1*V0 + 2*W1) / (2 + 1).

dove:

  • W0 è il valore attuale smussato della sequenza P;
  • V0 è il valore attuale dell'oscillazione della sequenza P;
  • W1 è il valore smussato precedente.

Nel Smoothed ADX, questo algoritmo di smussamento viene applicato a tutti e tre i buffer dell'indicatore ADX standard. Ecco perché l'indicatore ottenuto prende il nome di Smoothed ADX. Se avessimo smussato l'indicatore RSI, lo avremmo chiamato Smoothed RSI, e così via.

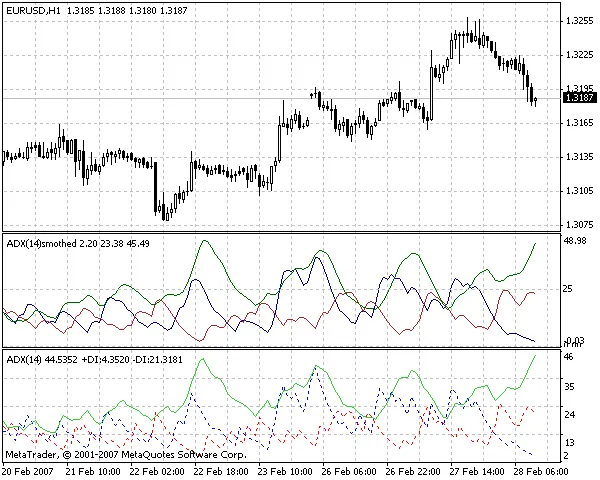
La figura qui sotto mostra che il Smoothed ADX è, in effetti, meno 'tremolante' rispetto all'ADX originale (Average Directional Movement Index).


Post correlati

Elenco
Commento (0)