Teoría:
El promedio móvil triangular es una especie de promedio móvil ponderado, conocido por ofrecer resultados muy suaves. En este tipo de promedio, se le da más peso a los valores centrales de los datos promediados. Por lo tanto, los coeficientes se distribuyen de manera específica. Aquí te dejo algunos ejemplos que ilustran claramente la progresión de los coeficientes:
periodo 1 : 1 periodo 2 : 1 1 periodo 3 : 1 2 1 periodo 4 : 1 2 2 1 periodo 5 : 1 2 3 2 1 periodo 6 : 1 2 3 3 2 1 periodo 7 : 1 2 3 4 3 2 1 periodo 8 : 1 2 3 4 4 3 2 1 periodo 9 : 1 2 3 4 5 4 3 2 1y así sucesivamente ...
Existen varias implementaciones y definiciones del promedio móvil triangular. Algunas son precisas y otras no lo son (las “imprecisas” no se dieron cuenta de que no se puede tener el mismo valor promedio para periodos impares y pares). Algunas son en realidad una interpretación curiosa de lo que se ha discutido sobre el promedio móvil triangular repetidamente. Los métodos precisos principalmente solo carecen de una cosa: se repiten una y otra vez, y para periodos más largos, la velocidad de ejecución se vuelve crítica.
Esta versión:
Soluciona el problema de la velocidad de ejecución mientras produce resultados precisos (no hay valores promedio iguales para periodos impares y pares :)).
Uso:
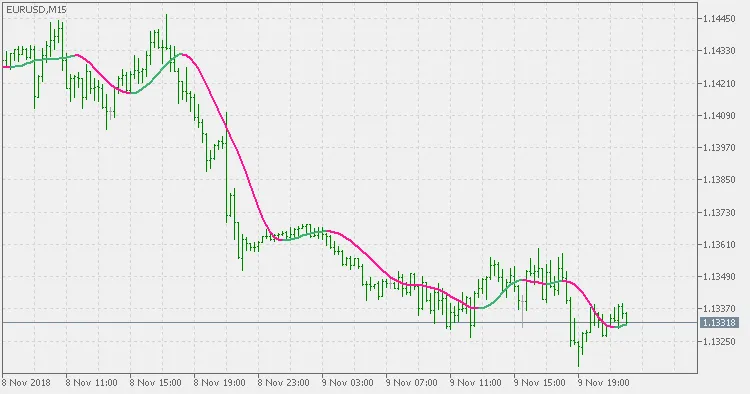
Puedes utilizar el cambio de color como señal. Ten en cuenta que, a diferencia de muchos que mezclan el TMA centrado con el TMA, este no es el TMA centrado y no recalcula ni repinta.