Panduan Lengkap Fractal Adaptive Moving Average (FrAMA) untuk MetaTrader 5

Fractal Adaptive Moving Average (FrAMA) adalah indikator teknikal yang dibangunkan oleh John Ehlers.

Indikator ini dibina berdasarkan algoritma Exponential Moving Average (EMA), di mana faktor pemulusan dikira berdasarkan dimensi fraktal semasa bagi siri harga. Kelebihan FrAMA adalah kemampuannya untuk mengikuti pergerakan trend yang kuat dan melambat pada saat-saat pengukuhan harga.

Semua jenis analisis yang digunakan untuk Moving Averages boleh diaplikasikan pada indikator ini.

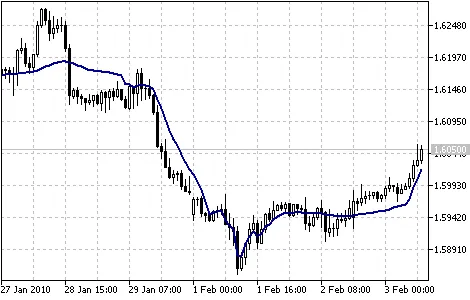
Indikator Fractal Adaptive Moving Average

Pengiraan:

FRAMA(i) = A(i) * Price(i) + (1 - A(i)) * FRAMA(i-1)

di mana:

FRAMA(i) - nilai semasa FrAMA;
Price(i) - harga semasa;
FRAMA(i-1) - nilai FrAMA sebelumnya;
A(i) - faktor pemulusan eksponensial semasa.

Faktor pemulusan eksponensial dikira dengan formula berikut:

A(i) = EXP(-4.6 * (D(i) - 1))

di mana:

D(i) - dimensi fraktal semasa;
EXP() - fungsi matematik eksponen.

Dimensi fraktal bagi garis lurus adalah sama dengan satu. Dari formula tersebut, jika D = 1, maka A = EXP(-4.6 *(1-1)) = EXP(0) = 1. Oleh itu, jika harga bergerak dalam garis lurus, pemulusan eksponensial tidak digunakan, kerana dalam kes ini formula kelihatan seperti ini:

FRAMA(i) = 1 * Price(i) + (1 - i) * FRAMA(i-1) = Price(i)

Ini bermakna indikator ini mengikuti harga dengan tepat.

Dimensi fraktal bagi pesawat adalah sama dengan dua. Dari formula, jika D = 2, maka faktor pemulusan A = EXP(-4.6*(2-1)) = EXP(-4.6) = 0.01. Nilai kecil bagi faktor pemulusan eksponensial ini diperoleh pada saat harga membuat pergerakan bergerigi yang kuat. Perlambatan yang kuat ini bersamaan dengan purata bergerak sederhana 200 tempoh.

Formula dimensi fraktal:

D = (LOG(N1 + N2) - LOG(N3))/LOG(2)

Ia dikira berdasarkan formula tambahan:

N(Length,i) = (HighestPrice(i) - LowestPrice(i))/Length

di mana:

HighestPrice(i) - nilai maksimum semasa untuk tempoh Length;
LowestPrice(i) - nilai minimum semasa untuk tempoh Length;

Nilai N1, N2 dan N3 masing-masing adalah sama dengan:

N1(i) = N(Length,i)
N2(i) = N(Length,i + Length)
N3(i) = N(2 * Length,i)

Panduan Lengkap Fractal Adaptive Moving Average (FrAMA) untuk MetaTrader 5

Siaran berkaitan