価格系列 x[i](i=1..n)の多調和(または多音)三角関数モデルは、以下のように表されます:
x[i] = m + Σ(a[h]*Cos(w[h]*i) + b[h]*Sin(w[h]*i), h=1..H)
ここで、
- x[i] - i番目のバーの過去価格、合計 n の過去価格;
- m - バイアス;
- a[h] と b[h] - 調和のスケーリング係数;
- w[h] - 調和の周波数;
- h - 調和番号;
- H - フィッティングされた調和の総数。
このモデルをフィッティングすることは、m、a[h]、b[h]、および w[h] を見つけて、モデル化された値が実際の値に近づくようにすることを意味します。調和周波数 w[h] を見つけることが、三角関数モデルをフィッティングする際の最も難しい部分です。フーリエ級数の場合、これらの周波数は 2πh/n に設定されます。しかし、フーリエ外挿とは、単に n の過去価格を未来に繰り返すことを意味します。
このインジケーターは、クイン-フェルナンデスアルゴリズムを使用して調和周波数を見つけます。指定された総調和数 H に達するまで、三角関数系列の調和を一つずつフィッティングします。新しい調和をフィッティングした後、コーディングされたアルゴリズムは、更新されたモデルと実際の値との間の残差を計算し、その残差に新しい調和をフィッティングします。
このインジケーターには、以下の入力パラメーターがあります:
- Npast - 三角関数系列をフィッティングするための過去バーの数;
- Nfut - 予測される未来バーの数;
- Nharm - モデル内の調和の総数;
- FreqTOL - 周波数計算の許容誤差。
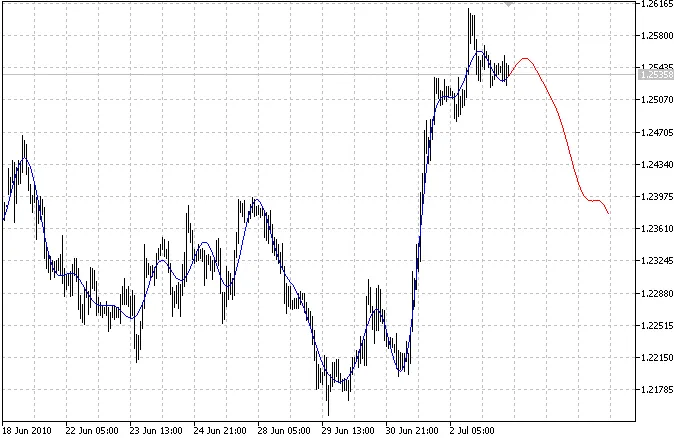
このインジケーターは、2つの曲線をプロットします。青い曲線はモデル化された過去の値を示し、赤い曲線はモデル化された未来の値を示しています。