Mastering the Variation Index: A Key Indicator for MetaTrader 5

Author:

The Variation Index is a handy tool that helps traders determine whether a trend is in play or if the market is moving sideways. It’s a great way to gauge market behavior, helping you make informed trading decisions.

In the world of trading, financial time series are among the most popular examples of fractal time functions. These series exhibit a fractal structure, and as the legendary Benoit Mandelbrot suggested, the movements of stocks and currencies often look similar when you zoom in or out on a market chart. This is something many traders have come to appreciate over time.

To figure out the fractal dimension, traders typically calculate the Hurst exponent. However, this requires a substantial amount of historical data—around 1,000 data points—which can be more than what you’d want to analyze for short-term trends.

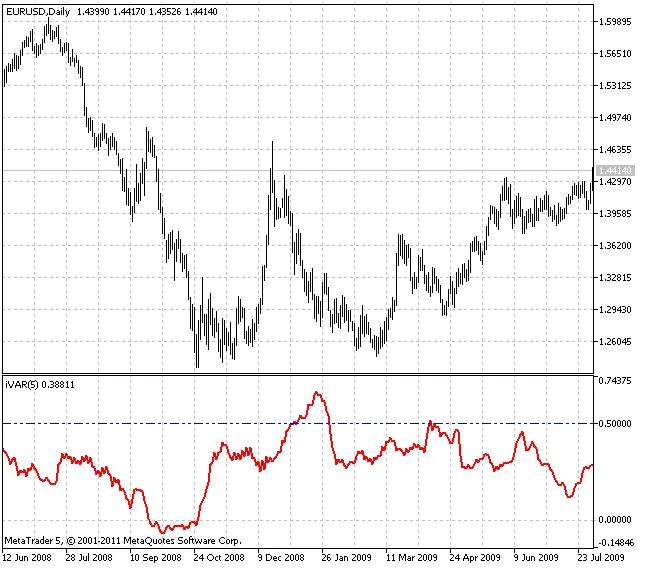
That’s where the Variation Index (m) comes into play. This index is closely tied to the fractal dimension but needs significantly less data to provide useful insights. Specifically, it allows traders to assess the dynamics of price series more locally. If the value of m is less than 0.5, you’re likely looking at a trending market; if it’s over 0.5, the market is probably flat.

The Variation Index indicator calculates based on a previous interval that is 2ⁿ long, with the parameter “n” set by you, the trader.

Here are some key rules for using the Variation Index:

If the indicator value is below 0.5, the market is trending.
A very low value may signal an impending correction in the current trend.
If the indicator is above 0.5, the market is flat.
A high value may indicate the start of a significant trend.
If the value is around 0.5, the market is in a state of uncertainty.

This indicator was first integrated into MQL4 and was published in the CodeBase at mql4.com on October 6, 2008.

Variation Index

References

Mastering the Variation Index: A Key Indicator for MetaTrader 5

Related Posts