Hoy vamos a explorar un indicador de tendencia que utiliza el análisis espectral singular, una herramienta poderosa para extraer tendencias y filtrar ruidos del mercado. Ajustar los parámetros de este indicador te permitirá controlar tanto la suavidad de la tendencia extraída como el umbral de filtrado de ruido.
El horizonte temporal de tu estrategia de trading juega un papel crucial, ya que determina cómo se segmentan los datos en componentes de tendencia, de baja frecuencia y de alta frecuencia, seguidos de la reconstrucción de señales. A diferencia de los métodos de filtrado convencionales, este indicador (tendencia suavizada) no presenta retrasos de fase, lo que te ofrece una visión más clara del mercado.
El indicador basado en el método "Caterpillar" descompone la serie de precios en componentes aditivos. Lo mejor es que no necesitas que la serie sea estacionaria, ni conocer el modelo de tendencia o la existencia de componentes periódicos y sus periodos.
Las capacidades de este indicador te permiten suavizar la serie, extraer la tendencia y, mediante la selección de parámetros de ajuste, filtrar las fluctuaciones "ruidosas" en escalas de tiempo más pequeñas.
Parámetros del Indicador
Los parámetros principales son:
- SegmentLength — longitud del fragmento de "historia reciente" en la serie de precios.
- SegmentLag — longitud de la "oruga". Se selecciona entre 1/4 y 1/2 de la longitud del fragmento. Afecta la discriminación de los componentes y la suavidad de la tendencia.
- EigMax — número de componentes principales (modos de descomposición). Define la dimensión del subespacio de señales y considera las fluctuaciones a diferentes escalas.
- EigNoiseFlag — bandera para calcular el número de componentes principales, que permite alternar entre un número "fijo" de modos y el valor del ruido permitido. Opciones = 0,1,2.
- EigNoiseLevel — porcentaje de ruido permitido en la "energía de fluctuación" total de la serie, si EigNoiseFlag != 0. Este parámetro anula el EigMax durante los cálculos.
Opciones del parámetro entero EigNoiseFlag:
- 0 - la dimensión del espacio de señales es fija: [1,EigMax] (se ignora EigNoiseLevel. Si EigMax es mayor que lo permitido, se limita al valor permitido).
- 1 — la proporción de un valor de modo individual respecto a la suma total de valores no es menor que el error especificado EigNoiseLevel. EigMax se selecciona automáticamente.
- 2 — considerar los modos con la proporción total diferente de "uno" (completa) no más que EigNoiseLevel.EigMax se selecciona automáticamente.
Selección típica e impacto de los parámetros:
- SegmentLength — longitud del fragmento de la serie de precios al final de la historia de datos. Se selecciona según la estabilidad de la historia y la naturaleza más o menos uniforme de los cambios en los datos o el periodo de la estrategia.
- SegmentLag — establece la dimensión para el "ancho de filtro" para modos individuales (inversamente proporcional). Afecta la suavidad y ajuste de la tendencia a la volatilidad del gráfico de precios.
- EigMax — establece la dimensión del subespacio de "señales" con información útil. Establece el umbral de "ruido".
- EigNoiseLevel — establece el valor de "ruido" en la dispersión total de la serie. Debe especificarse como un Porcentaje.
Implementación
La clase CCaterpillar implementada en el archivo CCaterpillar.mqh incluye todo lo necesario para el cálculo de la tendencia, excepto los procedimientos de álgebra lineal (se utiliza la biblioteca ALGLIB para la descomposición singular de la matriz de trayectoria). El código presentado en el archivo incluye descripciones para los miembros y procedimientos de la clase.
El funcionamiento del indicador requiere los archivos:
- 1) MQL5\Include\SSA\CCaterpillar.mqh
- 2) MQL5\Indicators\SingularMA.mq5
- La biblioteca ALGLIB (me uno a muchos que agradecen a Sergey Bochkanov por proporcionar esta maravillosa biblioteca de métodos numéricos)
Particularidades de uso
No se recomienda establecer un fragmento de datos mayor a 300 valores debido a la alta carga computacional. Es óptimo usar entre 150 y 200. Siempre puedes cambiar a otro periodo de cálculos en el gráfico para cubrir un intervalo de historia más grande.
Es aconsejable ajustar la ventana de la "oruga" en un rango de 1/3 a 1/2 de la longitud del fragmento. Si la ventana excede la mitad del fragmento, debido a la simetría de la trayectoria y la matriz transpuesta, esto es equivalente a un segmento con longitud simétrica respecto al medio del fragmento. Una longitud de ventana pequeña no proporciona un promedio cualitativo ni una separación de información por modos determinados.
Si hay un flujo lento de datos en la interfaz gráfica de la serie de precios, las posibles soluciones son: a) disminuir la longitud del fragmento; b) aumentar el parámetro ReCalcLim de la discreción de recalculo en la función OnCalculate.
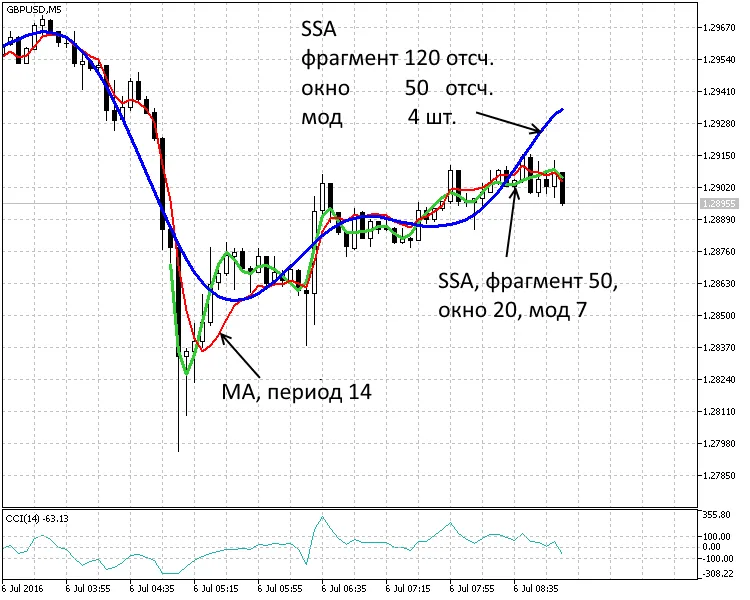
Fig.1. Periodo de 5 minutos. Dos tendencias SSA(120,50,4), SSA(50,20,7) y media móvil MA(14)
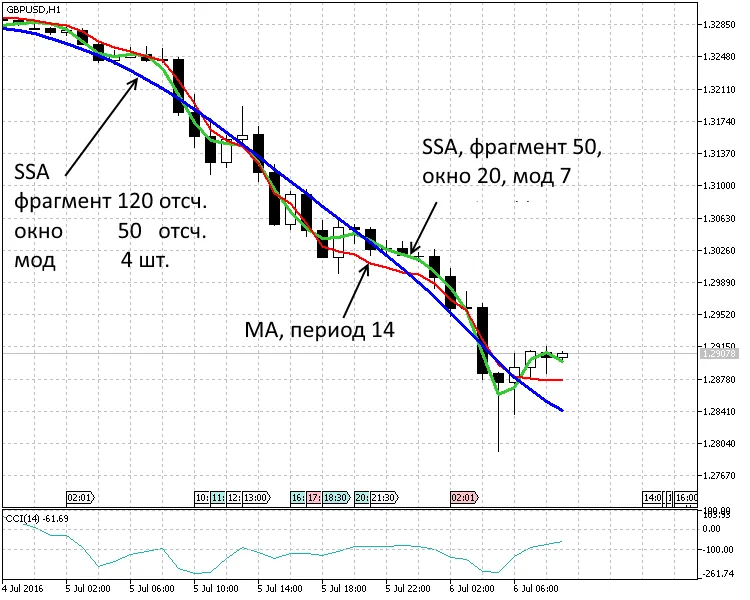
Fig. 2. Periodo de 1 hora. Dos tendencias SSA(120,50,4), SSA(50,20,7) y media móvil MA(14)
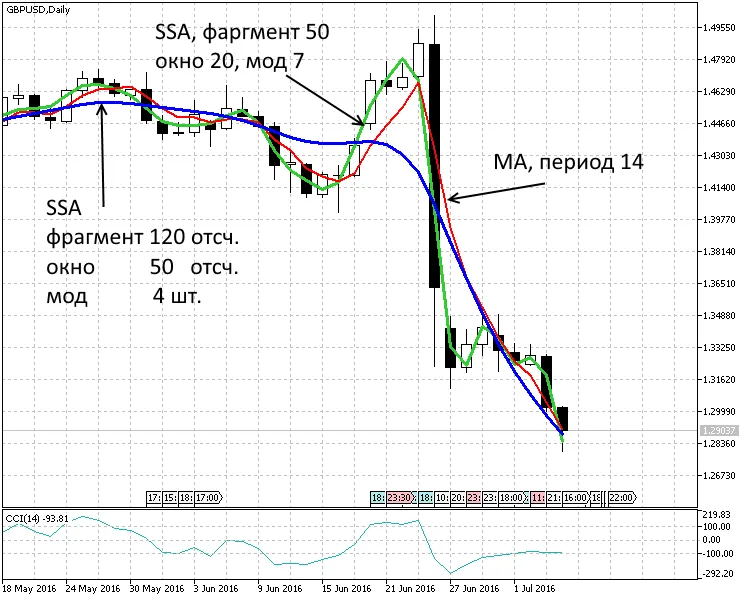
Fig. 3. Periodo de 1 día. Dos tendencias SSA(120,50,4), SSA(50,20,7) y media móvil MA(14)
El uso del análisis singular para implementar un indicador de tendencia en esta forma es una ilustración básica. El uso extendido de los métodos SSA en el sector financiero para el análisis y pronóstico de series temporales es bien conocido.
Referencias
- Elsner J.B., Tsonis A.A. Análisis Espectral Singular: Una Nueva Herramienta en el Análisis de Series Temporales. Plenum Press. Nueva York, 1996. 164 p.
- D. L. Danilov y A. A. Zhiglyavskii Componentes Principales en Series Temporales: el Método de la Oruga. Universidad Estatal de San Petersburgo, San Petersburgo, 1997 -308 p.
- N. E. Golyandina El método "Caterpillar"-SSA: análisis de series temporales: Guía de Estudio. San Petersburgo: 2004. - 76 p.
- Componentes Principales en Series Temporales: el Método de la Oruga, editado por D. L. Danilov, A. A. Zhigljavsky. San Petersburgo: Presskom, 1997. P. 308.
- Método de «Caterpillar»-SSA — ARIMA — SIGARCH y ARSIMA — SIGARCH modelo para el análisis y pronóstico de series temporales financieras y económicas: Actas de la Segunda Conferencia Científica Internacional "Métodos matemáticos, modelos y tecnologías de información en economía", 4-6 de mayo de 2011, Chernivtsi. — P. 306—308.
- Kozhihova N.A., Shiryaev V.I. Pronóstico de series temporales usando componentes caóticos. Boletín de la Universidad Estatal del Sur de los Urales, № 22, 2010, P. 22-25.
- A.M. Avdeenko Asesores e indicadores basados en los modelos SSA y generalizaciones no lineales // ver. arXiv:

Comentarios 0