FRAMA หรือ Fractal Adaptive Moving Average เป็นตัวชี้วัดทางเทคนิคที่พัฒนาขึ้นโดย John Ehlers เพื่อช่วยนักเทรดในการวิเคราะห์ตลาดได้อย่างมีประสิทธิภาพมากขึ้น.
ตัวชี้วัดนี้สร้างขึ้นจากอัลกอริธึมของ ค่าเฉลี่ยเคลื่อนที่แบบเอ็กซ์โพเนเชียล (EMA) โดยมีการคำนวณปัจจัยการปรับความราบเรียบตามมิติแฟรคทัลของชุดราคาในขณะนั้น. ข้อดีของ FRAMA คือสามารถติดตามการเคลื่อนไหวของแนวโน้มที่แข็งแกร่งได้ดี และสามารถชะลอการเคลื่อนไหวได้ในช่วงที่ราคาเคลื่อนที่ในลักษณะคงที่.
การวิเคราะห์ทุกประเภทที่ใช้สำหรับค่าเฉลี่ยเคลื่อนที่สามารถนำมาใช้กับตัวชี้วัดนี้ได้.
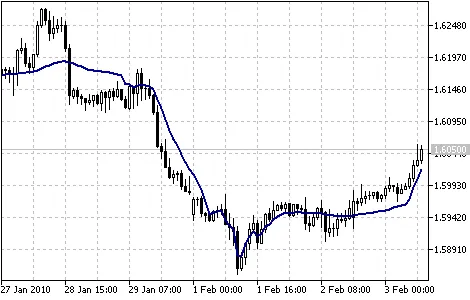
ตัวชี้วัด FRAMA
การคำนวณ:
FRAMA(i) = A(i) * Price(i) + (1 - A(i)) * FRAMA(i-1)
โดยที่:
- FRAMA(i) - ค่าปัจจุบันของ FRAMA;
- Price(i) - ราคาปัจจุบัน;
- FRAMA(i-1) - ค่าก่อนหน้าของ FRAMA;
- A(i) - ปัจจัยการปรับความราบเรียบแบบเอ็กซ์โพเนเชียลในขณะนั้น.
ปัจจัยการปรับความราบเรียบแบบเอ็กซ์โพเนเชียลคำนวณตามสูตรดังนี้:
A(i) = EXP(-4.6 * (D(i) - 1))
โดยที่:
- D(i) - มิติแฟรคทัลในขณะนั้น;
- EXP() - ฟังก์ชันทางคณิตศาสตร์ของเลขชี้กำลัง.
มิติแฟรคทัลของเส้นตรงเท่ากับหนึ่ง. จากสูตรถ้า D = 1, A = EXP(-4.6 * (1-1)) = EXP(0) = 1. ดังนั้นถ้าราคาเคลื่อนไหวในลักษณะเส้นตรง การปรับความราบเรียบแบบเอ็กซ์โพเนเชียลจะไม่ถูกใช้, เพราะในกรณีนี้สูตรจะมีลักษณะดังนี้:
FRAMA(i) = 1 * Price(i) + (1 - i) * FRAMA(i-1) = Price(i)
กล่าวคือ ตัวชี้วัดจะติดตามราคาตรงตามนั้น.
มิติแฟรคทัลของพื้นที่เท่ากับสอง. จากสูตรเราจะได้ว่าถ้า D = 2, ปัจจัยการปรับ A = EXP(-4.6*(2-1)) = EXP(-4.6) = 0.01. ค่าที่เล็กมากของปัจจัยการปรับแบบเอ็กซ์โพเนเชียลนี้จะเกิดขึ้นในช่วงที่ราคามีการเคลื่อนไหวแบบซิกแซกอย่างรุนแรง. การชะลอที่แข็งแกร่งนี้สอดคล้องกับค่าเฉลี่ยเคลื่อนที่แบบง่ายประมาณ 200 ช่วงเวลา.
สูตรของมิติแฟรคทัล:
D = (LOG(N1 + N2) - LOG(N3))/LOG(2)
คำนวณจากสูตรเสริม:
N(Length,i) = (HighestPrice(i) - LowestPrice(i))/Length
โดยที่:
- HighestPrice(i) - ค่าสูงสุดปัจจุบันในช่วง Length;
- LowestPrice(i) - ค่าต่ำสุดปัจจุบันในช่วง Length.
ค่าต่างๆ N1, N2 และ N3 จะมีค่าเท่ากับ:
N1(i) = N(Length,i)
N2(i) = N(Length,i + Length)
N3(i) = N(2 * Length,i)
