Fractal Adaptive Moving Average(フラクタル適応移動平均)、通称FrAMAは、ジョン・エイラーズによって開発されたテクニカルインジケーターです。
このインジケーターは、指数移動平均のアルゴリズムに基づいて構築されており、価格系列の現在のフラクタル次元に基づいてスムージング係数を計算します。FrAMAの利点は、強いトレンドの動きを追随し、価格の統合時には十分にスローダウンすることができる点です。
移動平均に応じた全ての分析手法は、このインジケーターにも適用できます。
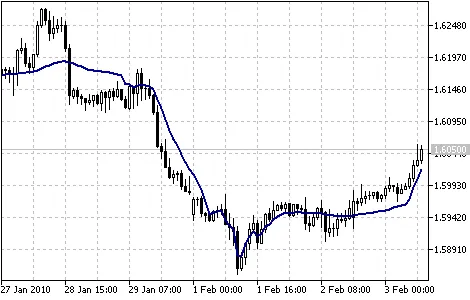
フラクタル適応移動平均インジケーター
計算方法:
FRAMA(i) = A(i) * Price(i) + (1 - A(i)) * FRAMA(i-1)
ここで:
- FRAMA(i) - 現在のFRAMAの値;
- Price(i) - 現在の価格;
- FRAMA(i-1) - 前回のFRAMAの値;
- A(i) - 現在の指数スムージング係数。
指数スムージング係数は、以下の式で計算されます:
A(i) = EXP(-4.6 * (D(i) - 1))
ここで:
- D(i) - 現在のフラクタル次元;
- EXP() - 指数の数学関数。
直線のフラクタル次元は1です。この式からわかるように、D = 1の場合、A = EXP(-4.6 * (1-1)) = EXP(0) = 1となります。つまり、価格が直線的に変動する場合、指数スムージングは使用されません。その場合、式は次のようになります:
FRAMA(i) = 1 * Price(i) + (1 - i) * FRAMA(i-1) = Price(i)
これは、インジケーターが価格に正確に追随することを意味します。
平面のフラクタル次元は2です。この式から、D = 2の場合、スムージング係数A = EXP(-4.6*(2-1)) = EXP(-4.6) = 0.01となります。このように小さな値の指数スムージング係数は、価格が強いノコギリ状の動きをする時に得られます。この強いスローダウンは、約200期間の単純移動平均に相当します。
フラクタル次元の公式:
D = (LOG(N1 + N2) - LOG(N3))/LOG(2)
これは、以下の追加の式に基づいて計算されます:
N(Length,i) = (HighestPrice(i) - LowestPrice(i))/Length
ここで:
- HighestPrice(i) - 現在のLength期間の最大値;
- LowestPrice(i) - 現在のLength期間の最小値。
N1、N2、N3の値はそれぞれ次のようになります:
N1(i) = N(Length,i)
N2(i) = N(Length,i + Length)
N3(i) = N(2 * Length,i)
