Entendendo o Indicador ADX Suavizado de John Ehlers

O Indicador ADX Suavizado foi desenvolvido a pedido de um visitante em um fórum, e a sua criação não foi muito complicada. No entanto, a busca por uma descrição clara do algoritmo do ADX suavizado não trouxe resultados. Por isso, vou compartilhar aqui o código que foi fornecido:

Entradas: {definindo entradas}
Length(14), ADXTrend(25), alpha1(0.25), alpha2(0.33);

Variáveis: {definindo variáveis}
     DMIPlus(0), DMIMinus(0), DMI(0), ADX(0),
     DIPlusLead(0), DIMinusLead(0), DIPlusFinal(0), DIMinusFinal(0),
     ADXLead(0), ADXFinal(0);

{agora chamando as funções internas do ADX, para que não precisemos calculá-las}

Value1 = DirMovement(H, L, C, Length, DMIPlus, DMIMinus, ADX);

{esta parte é a suavização do indicador ADX original, as linhas DI+, DI- e ADX são suavizadas}

DIPlusLead = 2*DMIPlus + (alpha1 - 2) * DMIPlus[1] + (1 - alpha1) * DIPlusLead[1];
DIPlusFinal = alpha2*DIPlusLead + (1 - alpha2) * DIPlusFinal[1];

DIMinusLead = 2*DMIMinus + (alpha1 - 2) * DMIMinus[1] + (1 - alpha1) * DIMinusLead[1];
DIMinusFinal = alpha2*DIMinusLead + (1 - alpha2) * DIMinusFinal[1];

ADXLead = 2*ADX + (alpha1 - 2) * ADX[1] + (1 - alpha1) * ADXLead[1];
ADXFinal = alpha2*ADXLead + (1 - alpha2) * ADXFinal[1];

{Plotando no gráfico}

Plot1(DIPlusFinal, "DMI+");
Plot2(DIMinusFinal, "DMI-");
Plot3(ADXFinal, "ADX");

De fato, se você não se aprofundar no sentido subjacente do texto inicial sobre o ADX suavizado, essa suavização pode ser dividida em duas etapas. Suponha que temos uma sequência numérica P e precisamos suavizá-la com o mínimo de atraso. Para isso, construímos na primeira etapa a função V(P) da oscilação da sequência P a partir da seguinte fórmula:

V0 = (8*P0 - 7*P1 + 3*V1) / 4,
onde:

P0 é o valor atual da sequência (um preço ou um indicador);
P1 é o valor anterior da sequência;
V1 é o valor anterior da oscilação;
V0 é o valor atual da oscilação.

Ou, de outra forma:

     V0 = (Vol(P) + 3*V1) / 4,
onde:

     Vol(P) = 8*P0 - 7*P1 - explosão de Ehlers (o termo foi inventado por mim).

Na segunda etapa, aplicamos a suavização ponderada simples:

W0 = (1*V0 + 2*W1) / (2 + 1).
onde:

W0 é o valor suavizado atual da sequência P;
V0 é o valor atual da oscilação da sequência P;
W1 é o valor suavizado anterior.

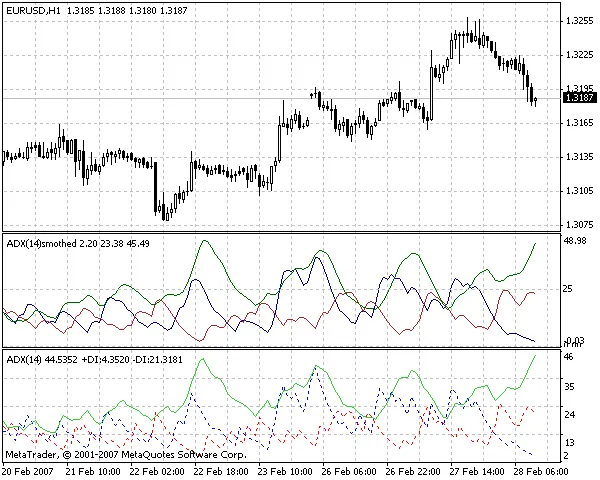
No ADX Suavizado, esse algoritmo de suavização é aplicado a todos os três buffers do indicador padrão ADX. É por isso que o indicador obtido é chamado de ADX Suavizado. Se estivéssemos suavizando o indicador RSI, o chamaríamos de RSI Suavizado, e assim por diante. A figura abaixo mostra que o ADX Suavizado, de fato, não é tão "tremido" quanto o ADX original, padrão (Average Directional Movement Index).

Entendendo o Indicador ADX Suavizado de John Ehlers

Publicações relacionadas