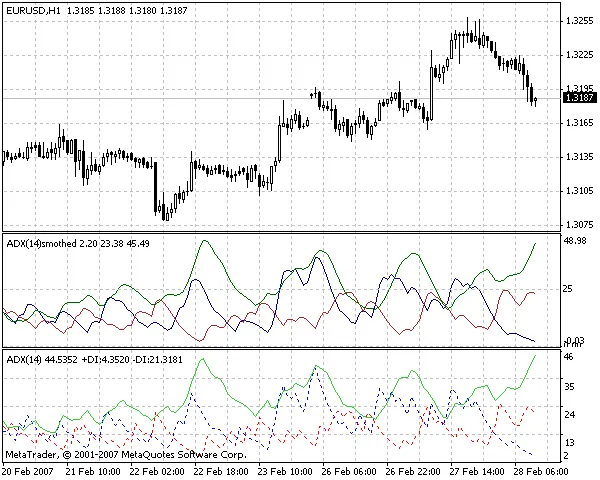
¡Hola a todos, traders! Hoy les traigo un indicador que muchos han estado esperando: el Smoothed ADX. Este indicador fue creado a petición de un miembro de nuestro foro y, aunque no fue complicado hacerlo, no encontré mucha información sobre su algoritmo. Así que, aquí les comparto el código que he preparado.
Entradas: {declarando entradas}
Longitud( 14 ),
ADXTrendy( 25 ), alpha1(0.25), alpha2(0.33);
DMIPlus( 0 ), DMIMinus( 0 ), DMI( 0 ), ADX( 0 ),
DIPlusLider(0), DIMinusLider(0), DIPlusFinal(0), DIMinusFinal(0),
ADXLider(0), ADXFinal(0);
DIPlusFinal = alpha2*DIPlusLider + (1 - alpha2) * DIPlusFinal[1];
DIMinusFinal = alpha2*DIMinusLider + (1 - alpha2) * DIMinusFinal[1];
ADXFinal = alpha2*ADXLider + (1 - alpha2) * ADXFinal[1];
Plot3( ADXFinal, "ADX" ) ;
Si no profundizamos en el sentido del Smoothed ADX, podemos dividir este suavizado en dos etapas. Imaginemos que tenemos una secuencia numérica P y necesitamos suavizarla con un mínimo de retardo. En la primera etapa, construimos la función V(P) de la secuencia P utilizando la siguiente fórmula:
V0 = (8*P0 - 7*P1 + 3*V1) / 4,
donde:
- P0 es el valor actual de la secuencia (un precio o un indicador);
- P1 es el valor anterior de la secuencia;
- V1 es el valor anterior de oscilación;
- V0 es el valor actual de oscilación.
O, de otra manera:
V0 = (Vol(P) + 3*V1) / 4,
donde:
Vol(P) = 8*P0 - 7P1 - el "estallido de Ehlers" (un término que he inventado).
En la segunda etapa, aplicamos un suavizado ponderado simple:
W0 = (1*V0 + 2*W1) / (2 + 1).
donde:
- W0 es el valor suavizado actual de la secuencia P;
- V0 es el valor actual de oscilación de la secuencia P;
- W1 es el valor suavizado anterior.