이론:
삼각 이동 평균은 부드러운 결과로 잘 알려진 가중 이동 평균의 일종입니다. 삼각 이동 평균은 중심값에 더 많은 가중치를 부여하여 최종 평균값에 영향을 미치도록 설계되어 있습니다. 이로 인해 계수는 특정하게 분배됩니다. 다음은 계수의 진행을 명확히 보여주는 몇 가지 예시입니다:
주기 1 : 1 주기 2 : 1 1 주기 3 : 1 2 1 주기 4 : 1 2 2 1 주기 5 : 1 2 3 2 1 주기 6 : 1 2 3 3 2 1 주기 7 : 1 2 3 4 3 2 1 주기 8 : 1 2 3 4 4 3 2 1 주기 9 : 1 2 3 4 5 4 3 2 1계속해서 진행됩니다...
삼각 이동 평균에 대한 여러 구현과 정의가 있습니다. 어떤 것들은 정확하고, 어떤 것들은 그렇지 않습니다(정확하지 않은 것들은 홀수와 짝수 주기에 대해 동일한 평균값을 가질 수 없다는 사실을 깨닫지 못했습니다). 실제로는 삼각 이동 평균에 대해 자주 언급되는 비틀린 해석도 존재합니다. 정확한 방법들은 주로 한 가지가 부족합니다: 반복적으로 계산을 하다 보니 긴 주기에서는 실행 속도가 중요해집니다.
이 버전:
정확한 결과를 생성하면서 실행 속도 문제를 해결합니다 (홀수와 짝수 주기에 대해 동일한 평균값이 없습니다 :))
사용법:
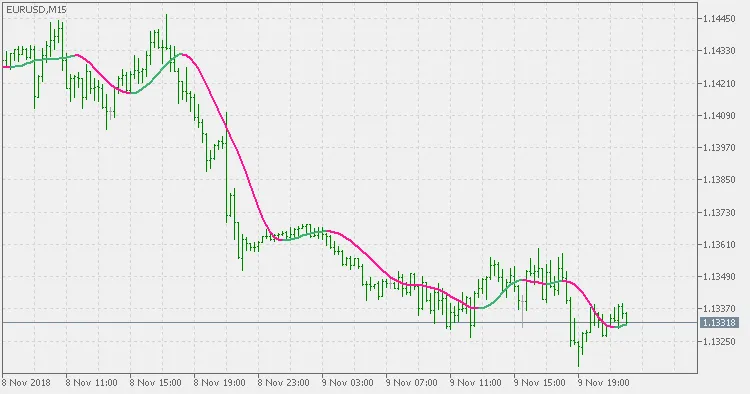
색상 변화를 신호로 사용할 수 있습니다. 많은 사람들이 센터드 TMA와 TMA를 혼합하는 것과는 달리, 이 지표는 센터드 TMA가 아니며 재계산/재표시하지 않습니다.