トリプル指数移動平均(TEMA)は、パトリック・マロイによって開発され、「Technical Analysis of Stocks & Commodities」という雑誌に掲載されました。
TEMAの計算原理は、ダブル指数移動平均(DEMA)に似ていますが、名前の通りのアルゴリズムではありません。この指標は、単純、二重、三重の指数移動平均を組み合わせたもので、それぞれ単独で使用する場合よりも遅れが少ないのが特徴です。
TEMAは、従来の移動平均の代わりに使用でき、価格データの平滑化や他の指標の平滑化にも利用できます。
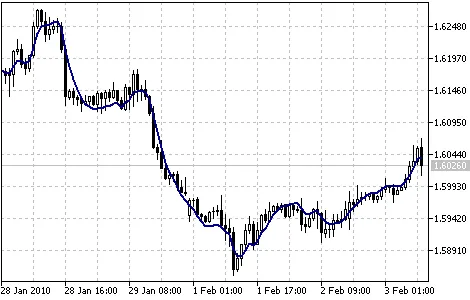
トリプル指数移動平均インジケーター
計算方法:
まず、DEMAを計算し、その後価格とDEMAとの偏差を求めます:
err(i) = Price(i) - DEMA(Price, N, ii)
ここで:
- err(i) - 現在のDEMA誤差;
- Price(i) - 現在の価格;
- DEMA(Price, N, i) - N期間の価格系列から得られる現在のDEMA値。
次に、誤差の指数平均を追加してTEMAを求めます:
TEMA(i) = DEMA(Price, N, i) + EMA(err, N, i) = DEMA(Price, N, i) + EMA(Price - EMA(Price, N, i), N, i) =
= DEMA(Price, N, i) + EMA(Price - DEMA(Price, N, i), N, i) = 3 * EMA(Price, N, i) - 3 * EMA2(Price, N, i) + EMA3(Price, N, i)
= DEMA(Price, N, i) + EMA(Price - DEMA(Price, N, i), N, i) = 3 * EMA(Price, N, i) - 3 * EMA2(Price, N, i) + EMA3(Price, N, i)
ここで:
- EMA(err, N, i) - 現在の誤差の指数平均の値;
- EMA2(Price, N, i) - 現在の二重価格平滑化の値;
- EMA3(Price, N, i) - 現在の三重価格平滑化の値。
