シングルスペクトラム分析の手法を用いてトレンドを抽出し、ノイズをフィルタリングします。インジケーターのパラメータを調整することで、抽出したトレンドの滑らかさやノイズのフィルタリング閾値をコントロールできます。
トレーディング戦略の時間軸に応じて、データをトレンド、低周波成分、高周波成分に最適に分解し、信号を再構成します。このインジケーター(平滑化されたトレンド)は、従来のフィルタリング手法や移動平均と異なり、位相遅延がありません。
「キャタピラー」手法に基づくトレンドインジケーターは、価格系列を加法的成分に展開します。この手法は、系列が定常である必要がなく、トレンドモデルや周期成分の存在に関する情報を知らなくても使用できます。
開発されたインジケーターは、シリーズを平滑化し、トレンドを抽出します。また、初期の価格系列のモデルに対する調整パラメータを選択することで、オシレーターの寄与を小さな時間スケールで考慮し、「ノイズ」変動をフィルタリングします。
インジケーターのパラメータ
主なパラメータは以下の通りです:
- SegmentLength — 価格系列の「最新履歴」フラグメントの長さ。
- SegmentLag — キャタピラーの長さ。フラグメント長の1/4から1/2の範囲で選択します。成分の識別性とトレンドの滑らかさに影響します。
- EigMax — 主成分の数(分解モード)。信号のサブスペースの次元を定義し、異なるスケールの変動を考慮します。
- EigNoiseFlag — 主成分の数を計算するためのフラグで、「固定」モード数と許可されたノイズの値を切り替えます。オプション = 0,1,2。
- EigNoiseLevel — シリーズの全体的な「変動エネルギー」における許可されたノイズの割合。EigNoiseFlag != 0の場合に適用されます。計算中にEigMaxを上書きします。
EigNoiseFlag整数パラメータのオプション:
- 0 - 信号空間の次元は固定:[1,EigMax](EigNoiseLevelは無視されます。EigMaxが許可された値を超える場合、許可された値に制限されます)。
- 1 — 個々のモード値の全体の合計に対する割合が指定された誤差EigNoiseLevel以上である場合。EigMaxは自動的に選択されます。
- 2 — 合計シェアが「1」(完全)からEigNoiseLevelの差異が異なるモードを考慮します。EigMaxは自動的に選択されます。
パラメータの一般的な選択と影響:
- SegmentLength — データ履歴の末尾の価格系列フラグメントの長さ。履歴の安定性やデータまたは戦略期間の変化の性質に基づいて選択されます。
- SegmentLag — 個々のモードの「フィルタ幅」の次元を設定します(逆比例)。トレンドの滑らかさと価格チャートのボラティリティへの調整に影響します。
- EigMax — 有用な情報を持つ「信号」サブスペースの次元を設定します。「ノイズ」しきい値を設定します。
- EigNoiseLevel — シリーズの総分散における「ノイズ」値を設定します。パーセンテージとして指定する必要があります。
実装
CCaterpillarクラスはCCaterpillar.mqhファイルに実装されており、トレンド計算に必要なすべてを含んでいます(軌道行列のシングル分解にはALGLIBライブラリが使用されています)。ファイルに示されたコードには、クラスのメンバーと手順の説明が含まれています。
インジケーターの操作には以下のファイルが必要です:
- 1) MQL5\Include\SSA\CCaterpillar.mqh
- 2) MQL5\Indicators\SingularMA.mq5
- 多数の人々に感謝されているALGLIBライブラリ(数値計算手法の素晴らしいライブラリを提供してくれた謝意を込めて)
使用上の特性
計算負荷が高いため、300値を超えるデータフラグメントを設定することは推奨されません。最適なのは150-200です。より大きな履歴インターバルをカバーするために、別のチャートの期間に切り替えることができます。
「キャタピラー」ウィンドウはフラグメント長の1/3から1/2の範囲で変更することをお勧めします。ウィンドウがフラグメントの半分を超えると、軌道とその転置行列の対称性により、フラグメントの中央に対して対称な長さのセグメントと同等になります。小さなウィンドウ長は、特定のモードに情報を質的に平均化し、分割することはできません。
価格系列のグラフィカルインターフェイスでデータの流れが遅い場合の解決策には、a)フラグメント長を減少させる、b)ReCalcLimパラメータを増加させることが含まれます。
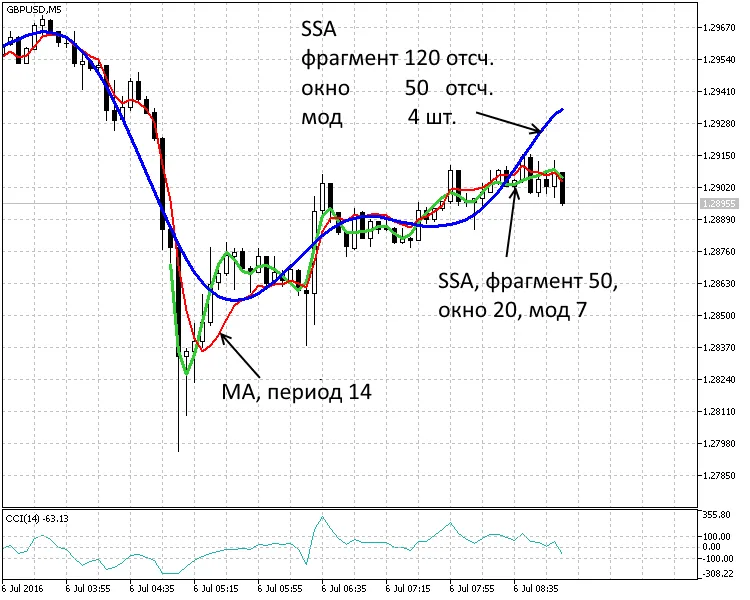
図1. 5分の期間。2つのトレンドSSA(120,50,4)、SSA(50,20,7)と移動平均MA(14)
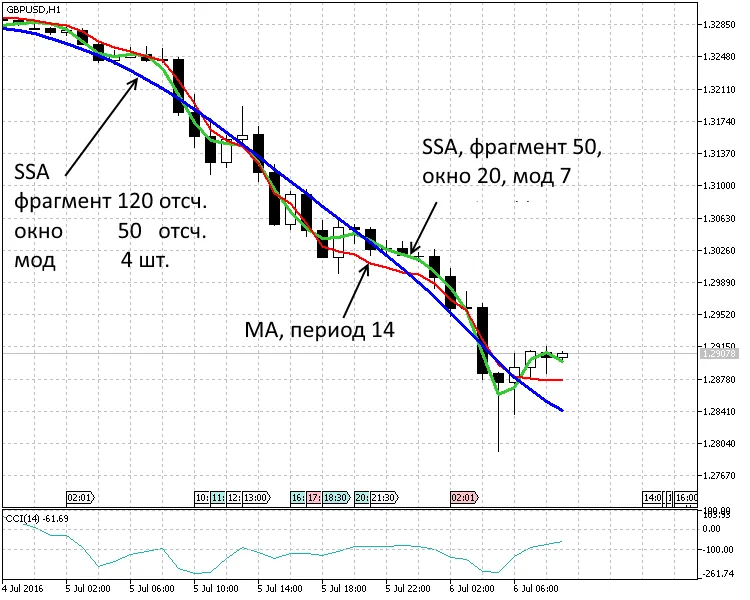
図2. 1時間の期間。2つのトレンドSSA(120,50,4)、SSA(50,20,7)と移動平均MA(14)
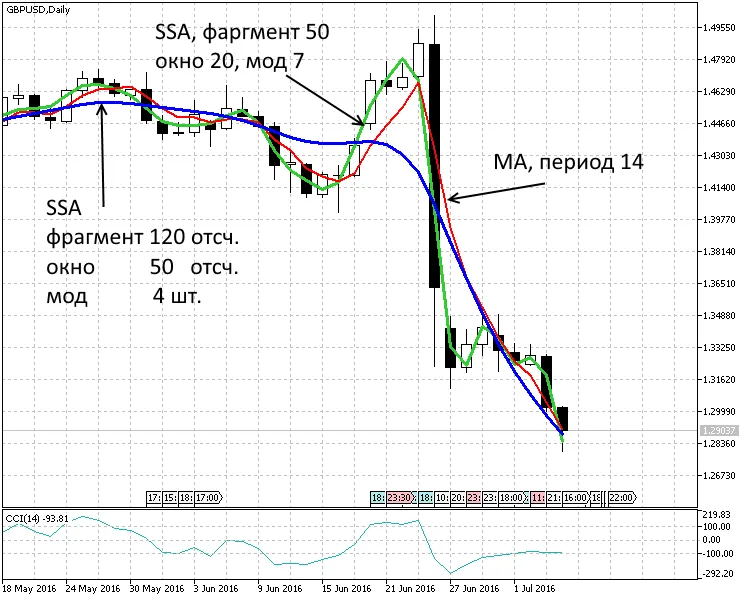
図3. 1日の期間。2つのトレンドSSA(120,50,4)、SSA(50,20,7)と移動平均MA(14)
この形式でのトレンドインジケーター実装のためのシングル分析の使用は基本的な例です。金融セクターにおけるSSA手法の広範な使用は、時間系列の分析と予測において示されています。
参考文献
- Elsner J.B., Tsonis A.A. シングルスペクトラム分析:時間系列分析の新しいツール。プレナムプレス。ニューヨーク、1996年。164ページ。
- D. L. Danilov and A. A. Zhiglyavskii 時間系列における主成分:キャタピラーメソッド。サンクトペテルブルク州立大学、サンクトペテルブルク、1997年 - 308ページ。
- N. E. Golyandina 「キャタピラー」-SSA法:時間系列の分析:学習ガイド。サンクトペテルブルク:2004年。 - 76ページ。
- 時間系列における主成分:キャタピラーメソッド、D. L. Danilov、A. A. Zhigljavskii編。サンクトペテルブルク:プレスコム、1997年。308ページ。
- 「キャタピラー」-SSA法の手法 — ARIMA — SIGARCHおよびARSIMA — SIGARCHモデルによる金融経済時間系列の分析と予測:第2回国際科学会議「経済における数学的方法、モデルおよび情報技術」、2011年5月4-6日、チェルニウツィ。 — 306-308ページ。
- Kozhihova N.A., Shiryaev V.I. カオス成分を使用した時間系列予測。南ウラル州立大学の公報、№ 22、2010年、22-25ページ。
- A.M. Avdeenko SSAモデルと非線形一般化に基づくアドバイザーおよびインジケーター // arXivを参照:

コメント 0