การใช้ค่าเฉลี่ยเคลื่อนที่สองเท่า (DEMA) เป็นเครื่องมือทางเทคนิคที่ถูกพัฒนาขึ้นโดย Patrick Mulloy และเผยแพร่ในเดือนกุมภาพันธ์ ปี 1994 ใน นิตยสาร 'Technical Analysis of Stocks & Commodities'
DEMA ถูกใช้เพื่อช่วยปรับเรียบราคาหุ้นและสามารถนำมาใช้ตรงบนกราฟราคาของทรัพย์สินทางการเงิน นอกจากนี้ยังสามารถใช้ปรับเรียบค่าของตัวชี้วัดอื่นๆ ได้อีกด้วย
ข้อดีของ DEMA คือมันช่วยลดสัญญาณผิดพลาดจากการเคลื่อนไหวของราคาแบบฟันเลื่อย และช่วยให้เราสามารถรักษาสถานะในช่วงแนวโน้มที่แข็งแกร่งได้
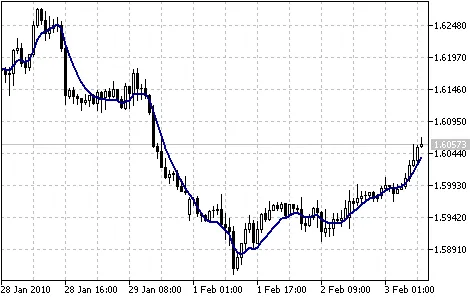
ตัวชี้วัดค่าเฉลี่ยเคลื่อนที่สองเท่า (DEMA)
การคำนวณ:
เครื่องมือนี้อิงจาก ค่าเฉลี่ยเคลื่อนที่แบบเอ็กซ์โพเนนเชียล (EMA) มาดูกันว่าความผิดพลาดของราคาที่เบี่ยงเบนจากค่า EMA คำนวณอย่างไร:
โดยที่:
- err(i) - ความผิดพลาดของ EMA ในปัจจุบัน;
- Price(i) - ราคาปัจจุบัน;
- EMA(Price, N, i) - ค่าของ EMA ในปัจจุบันของชุดราคาที่มีระยะเวลา N.
จากนั้นเราจะนำค่าความผิดพลาดเฉลี่ยแบบเอ็กซ์โพเนนเชียลมาบวกกับค่าของค่าเฉลี่ยเคลื่อนที่แบบเอ็กซ์โพเนนเชียลของราคาเพื่อให้ได้ DEMA:
= 2 * EMA(Price, N, i) - EMA(Price - EMA(Price, N, i), N, i) = 2 * EMA(Price, N, i) - EMA2(Price, N, i)
โดยที่:
- EMA(err, N, i) - ค่าปัจจุบันของค่าเฉลี่ยเคลื่อนที่แบบเอ็กซ์โพเนนเชียลของความผิดพลาด err;
- EMA2(Price, N, i) - ค่าปัจจุบันของการปรับเรียบราคาที่ย้อนหลังสองครั้ง.
