त्रैतीय गुणनात्मक चलन औसत (TEMA) तकनीकी संकेतक पैट्रिक मुलॉय द्वारा विकसित किया गया था और इसे "Technical Analysis of Stocks & Commodities" पत्रिका में प्रकाशित किया गया था।
TEMA की गणना का सिद्धांत द्विगुणित गुणनात्मक चलन औसत (DEMA) के समान है। नाम "त्रैतीय गुणनात्मक चलन औसत" वास्तव में इसके एल्गोरिदम को सही तरीके से नहीं दर्शाता है। यह एक अद्वितीय मिश्रण है जिसमें एकल, द्विगुणित और त्रैतीय गुणनात्मक औसत का समावेश होता है, जो प्रत्येक से कम विलंब प्रदान करता है।
TEMA को पारंपरिक चलन औसत के स्थान पर इस्तेमाल किया जा सकता है। इसे मूल्य डेटा को चिकना करने के लिए, साथ ही अन्य संकेतकों को चिकना करने के लिए भी उपयोग किया जा सकता है।
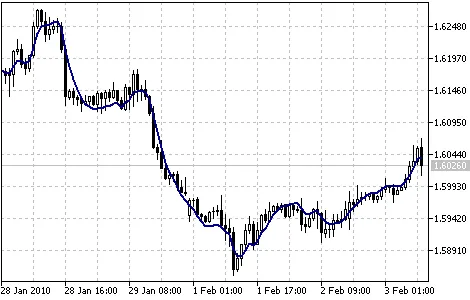
त्रैतीय गुणनात्मक चलन औसत संकेतक
गणना:
सबसे पहले DEMA की गणना की जाती है, फिर DEMA से मूल्य विचलन की त्रुटि की गणना की जाती है:
जहाँ:
- err(i) - वर्तमान DEMA त्रुटि;
- Price(i) - वर्तमान मूल्य;
- DEMA(Price, N, i) - मूल्य श्रृंखला से N अवधि का वर्तमान DEMA मान।
फिर त्रुटि के गुणनात्मक औसत का मान जोड़ें और TEMA प्राप्त करें:
= DEMA(Price, N, i) + EMA(Price - DEMA(Price, N, i), N, i) = 3 * EMA(Price, N, i) - 3 * EMA2(Price, N, i) + EMA3(Price, N, i)
जहाँ:
- EMA(err, N, i) - err त्रुटि का वर्तमान गुणनात्मक औसत मान;
- EMA2(Price, N, i) - वर्तमान द्विगुणित मूल्य चिकनाई;
- EMA3(Price, N, i) - वर्तमान त्रैतीय मूल्य चिकनाई।
