简介
有许多程序可以创建自相似集合,这些集合由迭代函数系统(IFS)定义。例如,Fractint、Fractal Designer,或IFS Matlab Generator等。由于MQL5语言的速度以及与图形对象的兼容性,这些美丽的集合可以在MetaTrader 5客户端终端中进行研究。
由cIntBMP库开发的图形功能大大简化了图形图像的创建。这一库获得了MetaQuotes Software Corp的特别奖。
在本篇文章中,我们将考察如何使用cIntBMP库进行工作,并探讨使用迭代函数系统创建分形集合的算法。
1. 平面的仿射变换
平面的仿射变换是一种映射 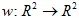 。通常,仿射2D变换可以通过一些
。通常,仿射2D变换可以通过一些 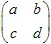 矩阵和
矩阵和 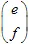 向量来定义。具有坐标(x,y)的点通过线性变换转变为其他点
向量来定义。具有坐标(x,y)的点通过线性变换转变为其他点 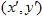 :
:
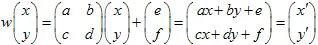
变换必须是非奇异的,即 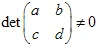 。仿射变换会将大小改变
。仿射变换会将大小改变 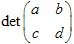 倍。
倍。
仿射变换不会改变几何对象的结构(线变换为线),AT允许描述对象的简单“变形”,如旋转、缩放和平移。
仿射平面变换的示例:
1) 平面的旋转 角度为:
2) 平面的缩放 采用
和
系数(X和Y轴):
3) 平面的平移 采用
向量:
收缩映射是关键(参见 Hutchinson 的结果)。
如果 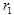 和
和 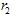 具有坐标
具有坐标 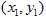 和
和 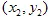 ,并且
,并且 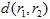 是一个度量(例如,欧几里得度量:
是一个度量(例如,欧几里得度量: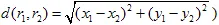 )。如果
)。如果 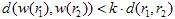 ,则称仿射变换为 收缩。
,则称仿射变换为 收缩。
以下是仿射变换的示例:

结果为:
2. 相似变换
通过以下方式构造分形:某些(简单的)几何对象(线段、三角形、正方形)分成N块,其中M块用于进一步的“构造”集合(如果N=M,我们将得到结果集的整数维数)。然后这个过程对每一块重复进行。
经典分形:
线段:
- 三分克赫曲线,N=3,M=4;
- 坎托尔尘埃,N=3,M=2;
三角形:
- 谢尔宾斯基垫片,N=4,M=3;
正方形:
- 谢尔宾斯基地毯,N=9,M=8;
- 维切克分形,N=9,M=5。
等等。
分形具有自相似结构,其中一些可以通过几个相似变换来定义。仿射变换的结构取决于分形构造的方式。
正如你将看到的那样,这非常简单,我们唯一需要解决的问题是只描述分形构造的第一个迭代,并找到相应的仿射变换集合。
假设我们有一个集合。根据分形创建算法,我们需要对其进行缩小、旋转并“放置在某个位置”。问题是使用仿射变换描述这个过程,即我们需要找到矩阵和向量。
可以很容易地证明,取初始集合的3个点(非平凡的)并将其变换为“缩小”集合的3个对应点是足够的。这个变换将导致6个线性方程,使我们能够找到a, b, c, d, e, f作为解。
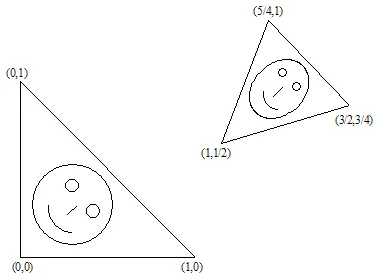
让我们来展示一下。假设 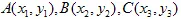 三角形转变为
三角形转变为 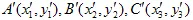 三角形。
三角形。
通过求解线性方程组,我们将能够得到a, b, c, d, e和f系数:
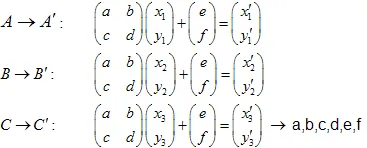
示例:谢尔宾斯基垫片:
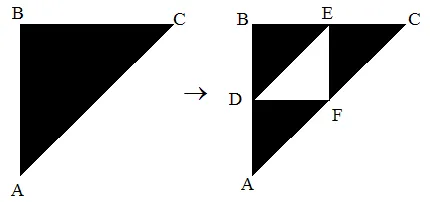
点的坐标是:
- A (0,0)
- B (0,1)
- C (1,1)
- D(0,1/2)
- E (1/2,1)
- F(1/2,1/2)
我们有3个变换:
- ABC -> ADF
- ABC -> DBE
- ABC -> FEC
线性方程组如下:
解决方案为:  ,
, 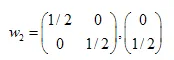 ,
, 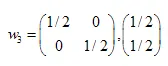
我们已经找到了三个仿射变换的系数。接下来,我们将用于创建自相似集合。
3. 使用迭代函数系统创建分形
迭代函数系统(IFS)是一组仿射收缩 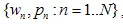 ,其中
,其中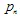 是“权重”。每个IFS函数由7个数字定义:
是“权重”。每个IFS函数由7个数字定义: 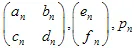 ,其中
,其中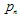 权重在迭代过程中用作第n次变换的概率。最好将它们的值定义为与收缩成比例:
权重在迭代过程中用作第n次变换的概率。最好将它们的值定义为与收缩成比例: 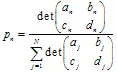 。
。
让我们考虑使用迭代函数系统构造分形的算法(另请参阅混沌游戏)。
首先,我们需要取一个初始点,坐标为 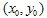 。接下来,我们随机选择一些收缩并绘制点
。接下来,我们随机选择一些收缩并绘制点 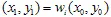 。然后再次随机选择一个收缩
。然后再次随机选择一个收缩 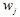 并绘制
并绘制 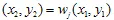 。最后我们将拥有
。最后我们将拥有 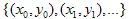 作为点集。
作为点集。
收缩的选择依赖于其“概率”。如果我们重复这个过程(例如,约30000个点)并绘制结果集,尽管这个过程是随机的,我们将看到其结构。
这里是一个谢尔宾斯基垫片的示例:
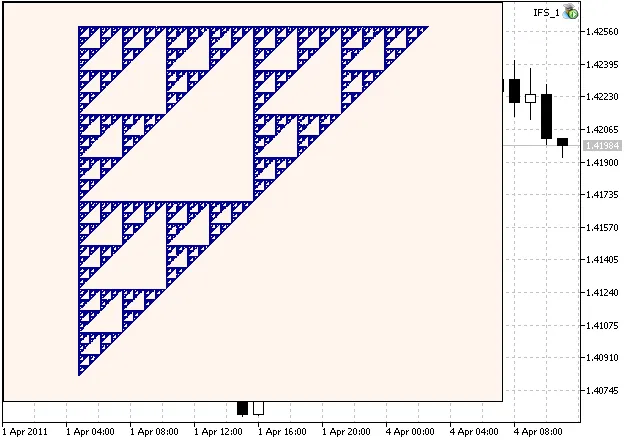
图 1. 使用章节2中计算的IFS系数生成的谢尔宾斯基垫片
代码如下:
//+------------------------------------------------------------------+//| IFS_Sierpinski_Gasket.mq5 |//| Copyright 2011, MetaQuotes Software Corp. |//| https://www.mql5.com |//+------------------------------------------------------------------+#property copyright "Copyright 2011, MetaQuotes Software Corp."#property link "https://www.mql5.com"#property version "1.00"//-- include file with cIntBMP class#include <cIntBMP.mqh>//-- Sierpinski Gasket IFS coefficients//-- (a,b,c,d) matriciesdouble IFS_a[3] = {0.50, 0.50, 0.50}; double IFS_b[3] = {0.00, 0.00, 0.00}; double IFS_c[3] = {0.00, 0.00, 0.00}; double IFS_d[3] = {0.50, 0.50, 0.50}; //-- (e,f) vectorsdouble IFS_e[3] = {0.00, 0.00, 0.50}; double IFS_f[3] = {0.00, 0.50, 0.50}; //--

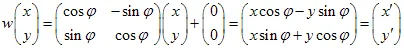
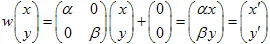
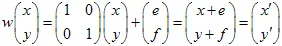
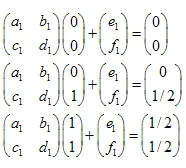

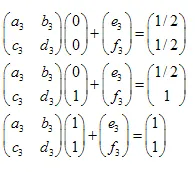
评论 0