Utiliser un Modèle ONNX pour Reconnaître des Chiffres Manuscrits sur MetaTrader 5

Un Expert Advisor pour la Reconnaissance de Chiffres Manuscrits

La base de données MNIST contient 60 000 images pour l'entraînement et 10 000 images pour les tests. Ces images proviennent d'un ensemble original de 20x20 pixels en noir et blanc, créé par le NIST, puis enrichi avec des échantillons de lycéens américains. Les échantillons ont été normalisés à une taille de 28x28 pixels, ce qui a introduit des niveaux de gris grâce à un traitement anti-aliasing.

Le modèle entraîné pour la reconnaissance de chiffres manuscrits, mnist.onnx, a été téléchargé depuis GitHub à partir de la Model Zoo (opset 8). Si vous êtes curieux, n'hésitez pas à télécharger et essayer d'autres modèles, en évitant ceux avec opset 1 qui ne sont plus supportés par le dernier runtime ONNX. Fait surprenant, le vecteur de sortie n'a pas été traité avec la fonction d'activation Softmax, ce qui est pourtant courant dans les modèles de classification. Pas de panique, nous pouvons facilement l'implémenter nous-mêmes.

int PredictNumber(void)
  {
   static matrixf image(28,28);
   static vectorf result(10);

   PrepareMatrix(image);

   if(!OnnxRun(ExtModel,ONNX_DEFAULT,image,result))
     {
      Print("OnnxRun error ",GetLastError());
      return(-1);
     }

   result.Activation(result,AF_SOFTMAX);
   int predict=int(result.ArgMax());
   if(result[predict]<0.8)
      Print(result);
      Print("valeur ",predict," prédite avec probabilité ",result[predict]);

   return(predict);
  }

Pour dessiner des chiffres, utilisez la souris tout en maintenant le bouton gauche enfoncé. Pour reconnaître le chiffre dessiné, appuyez sur le bouton CLASSIFIER.

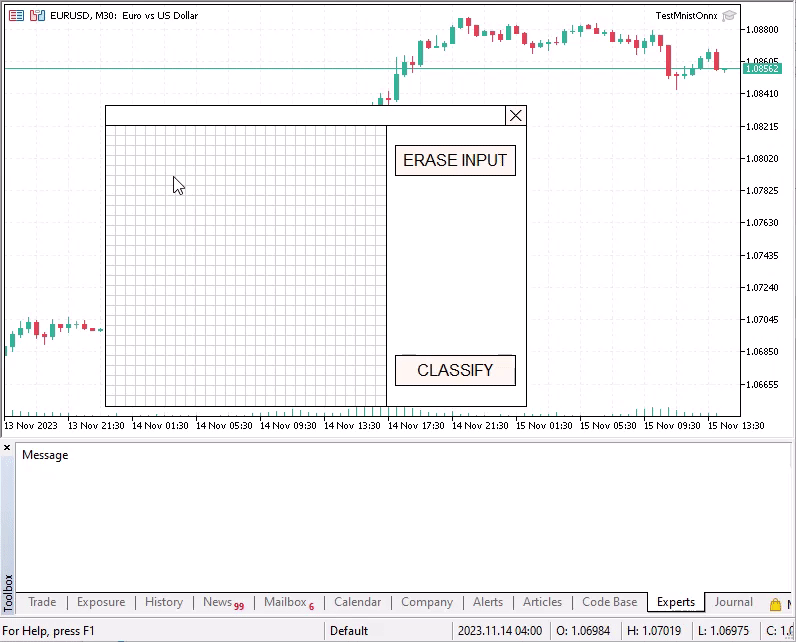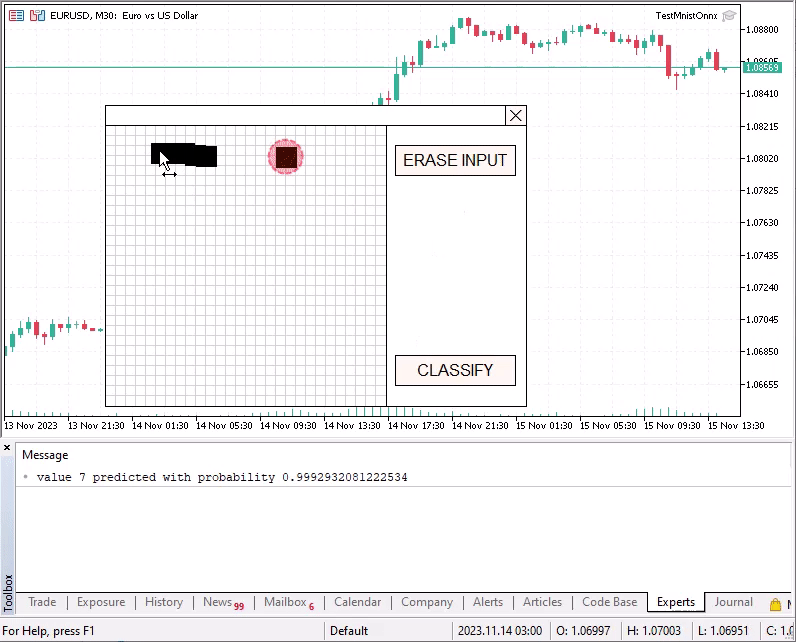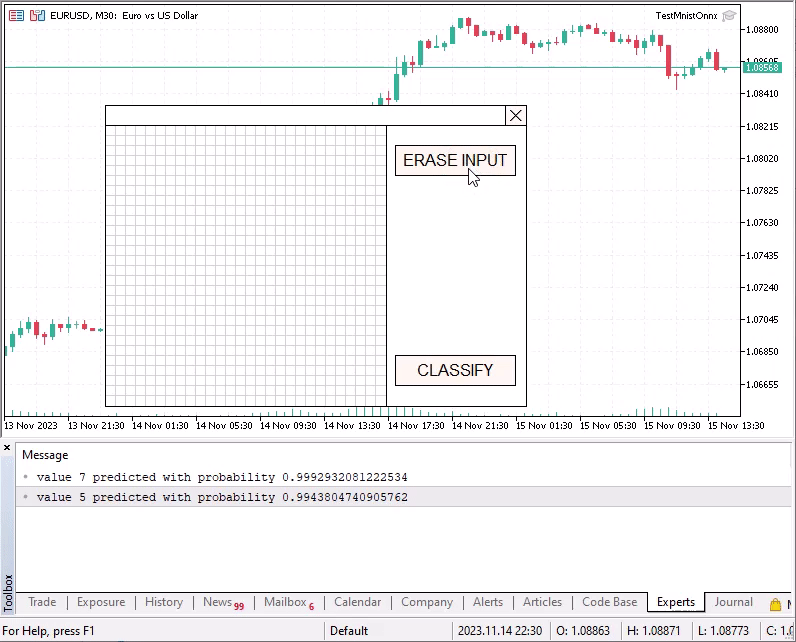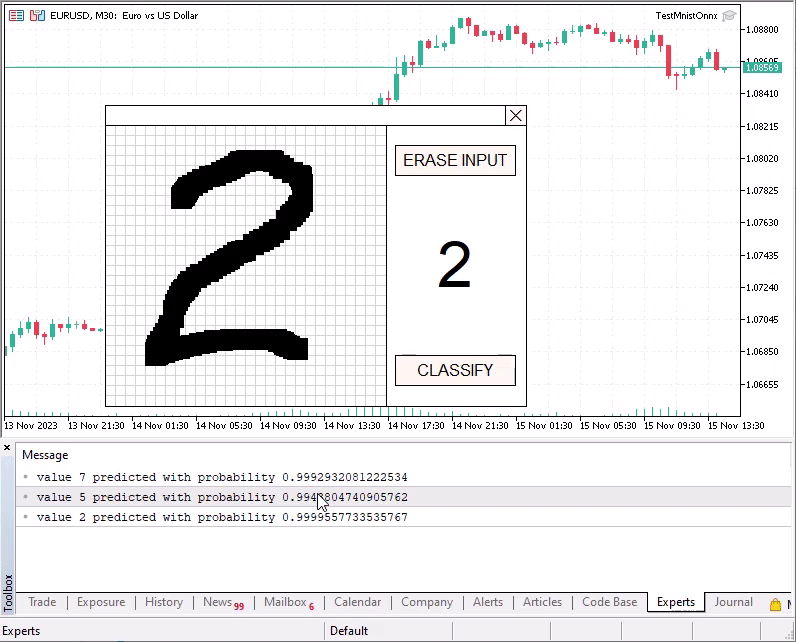
Si la probabilité obtenue pour le chiffre reconnu est inférieure à 0.8, le vecteur de résultats avec les probabilités pour chaque classe est affiché dans le journal. Par exemple, essayez de classifier un champ de saisie vide.

[0.095331445,0.10048489,0.10673151,0.10274081,0.087865397,0.11471312,0.094342403,0.094900772,0.10847695,0.09441267]
valeur 5 prédite avec probabilité 0.11471312493085861

En raison de certaines raisons, la précision de reconnaissance est particulièrement plus basse pour le chiffre neuf (9). Les chiffres inclinés vers la gauche sont reconnus avec plus de précision.

Utiliser un Modèle ONNX pour Reconnaître des Chiffres Manuscrits sur MetaTrader 5

Un Expert Advisor pour la Reconnaissance de Chiffres Manuscrits

Articles connexes