Introduction
In the world of trading, visually appealing and mathematically intriguing fractals can be a powerful tool. This guide will walk you through creating self-similar sets using the Iterated Function System (IFS) in MQL5, perfect for enhancing your MetaTrader 5 experience.
There are various applications out there for generating fractals, like Iterated Function System (IFS), each offering unique features. Some examples include Fractint, Fractal Designer, and the IFS Matlab Generator. With the speed of the MQL5 language, we can explore these stunning sets directly within the MetaTrader 5 client terminal.
The cIntBMP library, developed by Dmitry (Integer), opens up new graphic possibilities and simplifies the process of creating graphic images. This library has even been awarded a special prize by MetaQuotes Software Corp.
In this post, we'll dive into examples of working with the cIntBMP library and explore algorithms for creating fractal sets using Iterated Function Systems.
1. Affine Transformation of the Plane
Affine transformations are key to mapping points on a plane. Generally, an affine 2-D transform can be defined using a matrix and a vector. The point with coordinates (x, y) transforms to another point through linear transformation:
For the transformation to be effective, it must be non-singular. Affine transformations maintain the structure of geometric objects, allowing for simple deformations like rotation, scaling, and translation.
Examples of Affine Transformations:
- Rotation around an angle:
- Scaling with coefficients (X and Y axes):
- Translation of the plane by a vector:
The concept of contraction mappings is fundamental in this context.
2. Similarity Transforms
Fractals can be constructed by taking a geometric object (like a line segment or triangle), dividing it into N pieces, and using M of them to continue constructing the set. If N equals M, we achieve the integer dimension of the resulting set. This process can be repeated for each piece.
Classic Fractals:
- Triadic Koch Curve, N=3, M=4;
- Cantor Dust, N=3, M=2;
- Sierpinski Gasket, N=4, M=3;
- Sierpinski Carpet, N=9, M=8;
- Vichek Fractal, N=9, M=5.
These fractals exhibit self-similar structures, defined through various similarity transformations. The structure of an affine transform depends on how the fractal is constructed.
To create a fractal, we need to reduce, rotate, and position the initial set. This can be described using affine transformations, requiring us to find the appropriate matrix and vector.
By taking three non-trivial points from the initial set and transforming them to corresponding points in the reduced set, we arrive at six linear equations, allowing us to solve for the coefficients.
Let's consider the example of transforming a triangle into a smaller version:

3. Creating Fractals Using the Iterated Function Systems
The Iterated Function System (IFS) consists of a set of affine contractions, where each function is defined by seven numbers. These functions can be weighted to influence the transformation process.
The algorithm for fractal construction using IFS involves starting with an initial point and randomly selecting contractions to plot new points. Despite the randomness, repeating this process—say, 30,000 times—reveals the fractal's structure.
Check out this example of the Sierpinski Gasket:
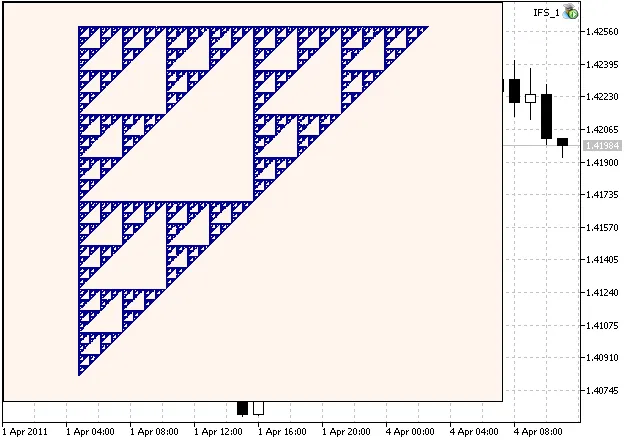
Here's the code to create the Sierpinski Gasket:
// Code snippet for creating Sierpinski Gasket
By tweaking the scale and increasing iterations, you can zoom into specific regions of the fractal to explore its self-similar structure further.
Another fascinating example is Barnsley's Fern, showcasing a more complex structure defined by a unique set of IFS contractions.

As you can see, even a limited number of coefficients can create stunningly intricate fractals.
Conclusion
We've explored the creation of self-similar sets using Iterated Function Systems, demonstrating how the cIntBMP library can simplify your work with graphic images. The potential for creating beautiful and complex fractal structures is vast.
As you experiment with these concepts, consider how you can extend your fractal creations—play with color palettes, zoom features, and even explore the fractal dimension of your designs.
Happy trading, and may your charts be as beautiful as the fractals you create!

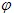
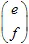
Comments 0