Home Trading Sistematico Post

Creazione di Frattali in MQL5 con Sistemi di Funzioni Iterati (IFS) per MetaTrader 5

Mike • 2011-04-15 03:35
20 0 0
Allegato
328.zip (16.56 KB, Scarica 0 volte)

Introduzione

Esistono molti programmi che permettono di creare insiemi auto-simili, definiti dai Sistemi di Funzioni Iterati (IFS). Ad esempio, puoi dare un'occhiata a Fractint, Fractal Designer o IFS Matlab Generator. Grazie alla velocità del linguaggio MQL5 e alla possibilità di lavorare con oggetti grafici, questi bellissimi insiemi possono essere studiati nel terminale MetaTrader 5.

La libreria cIntBMP, sviluppata da Dmitry (Integer), offre nuove opportunità grafiche e semplifica notevolmente la creazione di immagini grafiche. Questa libreria è stata premiata con un premio speciale da MetaQuotes Software Corp.

In questa pubblicazione, esploreremo alcuni esempi di utilizzo della libreria cIntBMP. Inoltre, tratteremo gli algoritmi per la creazione di insiemi frattali utilizzando i Sistemi di Funzioni Iterati.


1. Trasformazione Affine del Piano

La trasformazione affine del piano è una mappatura 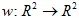. In generale, la trasformazione affine 2D può essere definita con una matrice 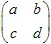e un vettore 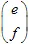. Il punto con coordinate (x,y) si trasforma in un altro punto 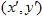usando la trasformazione lineare:

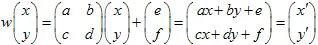
La trasformazione deve essere non singolare, il 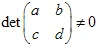. La trasformazione affine cambia la dimensione 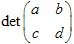volte.

Le trasformazioni affini non cambiano la struttura degli oggetti geometrici (le linee si trasformano in linee), l'AT consente di descrivere semplici "deformazioni" degli oggetti, come rotazione, scalatura e traslazione.

Esempi di trasformazioni affini del piano:

1) Rotazione del piano di un angolo :

2) Scalatura del piano con coefficienti e (assi X e Y):

3) Traduzione del piano con il vettore :

Le mappature contrattive sono fondamentali (vedi i risultati di Hutchinson).

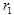Se e 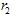hanno coordinat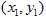e 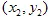e e 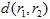è una metrica (ad esempio, la metrica euclidea: 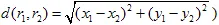). La trasformazione affine è chiamata contrattiva se 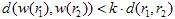, dove .

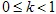Ecco un esempio di trasformazione affine:

Il risultato è:


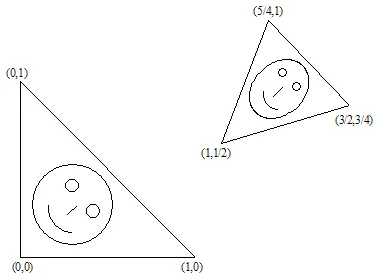
2. Trasformazioni di Somiglianza

I frattali sono costruiti nel modo seguente: un (semplice) oggetto geometrico (sezione, triangolo, quadrato) viene suddiviso in N pezzi e M di essi sono utilizzati per la "costruzione" successiva dell'insieme (se N=M, otteniamo la dimensione intera dell'insieme risultante). Questo processo viene quindi ripetuto di nuovo e ancora per ciascuno dei pezzi.

Frattali classici:

Sezioni:

  • Curva di Koch triadica, N=3, M=4;
  • Polvere di Cantor, N=3, M=2;

Triangolo:

  • Gasket di Sierpinski, N=4, M=3;

Quadrati:

  • Carpet di Sierpinski, N=9, M=8;
  • Frattale di Vichek, N=9, M=5.

e così via.

I frattali hanno una struttura auto-simile; alcuni di essi possono essere definiti da più trasformazioni di somiglianza. La struttura della trasformazione affine dipende dal modo di costruzione del frattale.

Come vedrai in seguito, è molto semplice, e l'unico problema da risolvere è descrivere solo la prima iterazione della costruzione del frattale e trovare il corrispondente insieme di trasformazioni affini.

Supponiamo di avere un certo insieme. Secondo l'algoritmo di creazione del frattale, dobbiamo ridurlo, ruotarlo e "metterlo in un certo posto". Il problema è descrivere questo processo usando trasformazioni affini, ovvero dobbiamo trovare la matrice e il vettore.

È facile dimostrare che è sufficiente prendere 3 punti dell'insieme iniziale (non banali) e trasformarli in 3 punti corrispondenti dell'insieme "ridotto". Questa trasformazione porterà a 6 equazioni lineari, permettendoci così di trovare a, b, c, d, e, f come soluzione.

Mostriamolo. Supponiamo che il triangolo 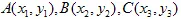venga trasformato nel triangolo .

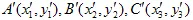Risolvendo il sistema di equazioni lineari, saremo in grado di ottenere i coefficienti a, b, c, d, e e f:

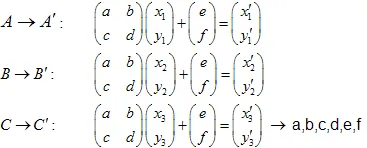
Esempio: Gasket di Sierpinski:

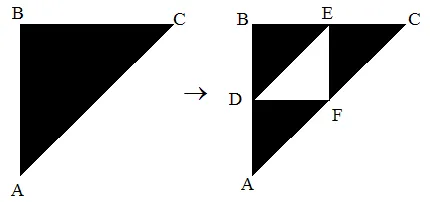
Le coordinate dei punti sono:

  • A (0,0)
  • B (0,1)
  • C (1,1)
  • D(0,1/2)
  • E (1/2,1)
  • F(1/2,1/2)

Abbiamo 3 trasformazioni:

  1. ABC -> ADF
  2. ABC -> DBE
  3. ABC -> FEC

Il sistema di equazioni lineari appare come segue:




Le soluzioni sono: , ,

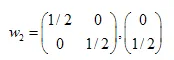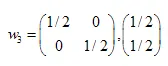
Abbiamo trovato i coefficienti di tre trasformazioni affini. In seguito li utilizzeremo per la creazione di insiemi auto-simili.


3. Creazione di Frattali Utilizzando i Sistemi di Funzioni Iterate

Il Sistema di Funzioni Iterati (IFS) è un insieme di contrazioni affini 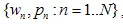dove 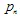sono i "pesi". Ciascuna delle funzioni IFS è definita da 7 numeri: 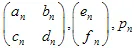, dove i pesi 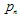sono utilizzati durante il processo di iterazione come probabilità della n-esima trasformazione. È meglio definire i loro valori, proporzionali alla contrazione: .

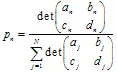Consideriamo l'algoritmo di costruzione del frattale utilizzando il Sistema di Funzioni Iterate (vedi anche Gioco del Caos).

Per prima cosa dobbiamo prendere un punto iniziale con coordinate 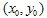. Poi, scegliamo casualmente alcune delle contrazioni e tracciamo il punto 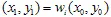. E di nuovo, scegliamo casualmente una delle contrazioni 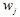e tracciamo 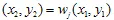. Infine avremo 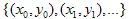come insieme di punti.

La scelta della contrazione dipende dalla sua "probabilità". Se ripetiamo il processo (ad esempio, per ~30000 punti) e tracciamo l'insieme risultante, vedremo la sua struttura nonostante il processo casuale.

Ecco un esempio del Gasket di Sierpinski:

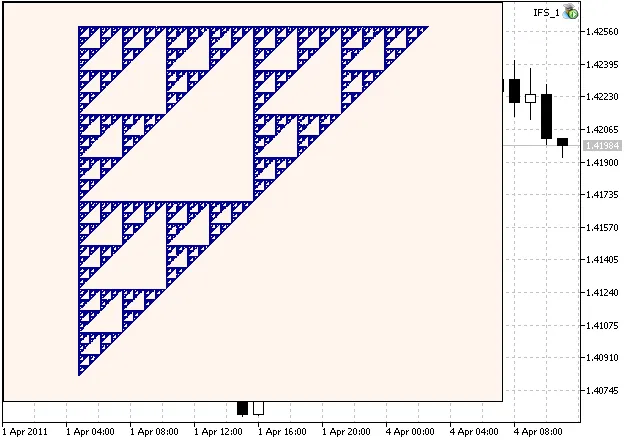
Figura 1. Il Gasket di Sierpinski, generato con i coefficienti IFS calcolati nel capitolo 2

Figura 1. Il Gasket di Sierpinski, generato con i coefficienti IFS calcolati nel capitolo 2

Il codice:

//+------------------------------------------------------------------+
//|                                              IFS_Sierpinski_Gasket.mq5 |
//|                                              Copyright 2011, MetaQuotes Software Corp. |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2011, MetaQuotes Software Corp."
#property link      "https://www.mql5.com"
#property version   "1.00"

//-- include file with cIntBMP class
#include <cIntBMP.mqh>

//-- Sierpinski Gasket IFS coefficients
//-- (a,b,c,d) matricies
double IFS_a[3] = {0.50,  0.50,  0.50};
double IFS_b[3] = {0.00,  0.00,  0.00};
double IFS_c[3] = {0.00,  0.00,  0.00};
double IFS_d[3] = {0.50,  0.50,  0.50};
//-- (e,f) vectors
double IFS_e[3] = {0.00,  0.00,  0.50};
double IFS_f[3] = {0.00,  0.50,  0.50};
//-- "probabilities" of transforms, multiplied by 1000
double IFS_p[3]={333,333,333};

double Probs[3]; // Probs array - used to choose IFS transforms
cIntBMP bmp;     // cIntBMP class instance
int scale=350;  // scale coefficient
//+------------------------------------------------------------------+
//| Expert initialization function                                               |
//+------------------------------------------------------------------+
int OnInit()
  {
//-- Prepare Probs array
   double m=0;
   for(int i=0; i<ArraySize(IFS_p); i++)
     {
      Probs[i]=IFS_p[i]+m;
      m=m+IFS_p[i];
     }
//-- size of BMP image
   int XSize=500;
   int YSize=400;
//-- create bmp image XSizexYSize with clrSeashell background color
   bmp.Create(XSize,YSize,clrSeashell);
//-- image rectangle
   bmp.DrawRectangle(0,0,XSize-1,YSize-1,clrBlack);

//-- point coordinates (will be used in construction of set)
   double x0=0;
   double y0=0;
   double x,y;
   //-- number of points to calculate (more points - detailed image)
   int points=1500000;
   //-- calculate set
   for(int i=0; i<points; i++)
     {
      // choose IFS tranform with probabilities, proportional to defined
      double prb=1000*(rand()/32767.0);
      for(int k=0; k<ArraySize(IFS_p); k++)
        {
         if(prb<=Probs[k])
           {
            // affine transformation
            x = IFS_a[k] * x0 + IFS_b[k] * y0 + IFS_e[k];
            y = IFS_c[k] * x0 + IFS_d[k] * y0 + IFS_f[k];
            // update previous coordinates
            x0 = x;
            y0 = y;
            // convert to BMP image coordinates
            // (note the Y axis in cIntBMP)
            int scX = int (MathRound(XSize/2 + (x-0.5)*scale));
            int scY = int (MathRound(YSize/2 + (y-0.5)*scale));
            // if the point coordinates inside the image, draw the dot
            if(scX>=0 && scX<XSize && scY>=0 && scY<YSize) { bmp.DrawDot(scX,scY,clrDarkBlue); }
            break;
         }
     }
     }
//-- save image to file
   bmp.Save("bmpimg",true);
//-- plot image on the chart
   bmp.Show(0,0,"bmpimg","IFS");
//---
   return(0);
  }
//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//--- delete image from the chart
   ObjectDelete(0,"IFS");
//--- delete file
   bmp.Delete("bmpimg",true);
  }
//+------------------------------------------------------------------+

Se impostiamo la scala a 1350, aumentiamo il numero di iterazioni a 15000000 e cambiamo lo spostamento del punto iniziale:

int scX = MathRound(XSize/2 + (x-0.75)*scale);
int scY = MathRound(YSize/2 + (y-0.75)*scale);

siamo in grado di vedere la regione ingrandita dell'insieme. Si può notare (Fig. 2) che ha una struttura auto-simile:

Figura 2. Regione ingrandita del Gasket di Sierpinski

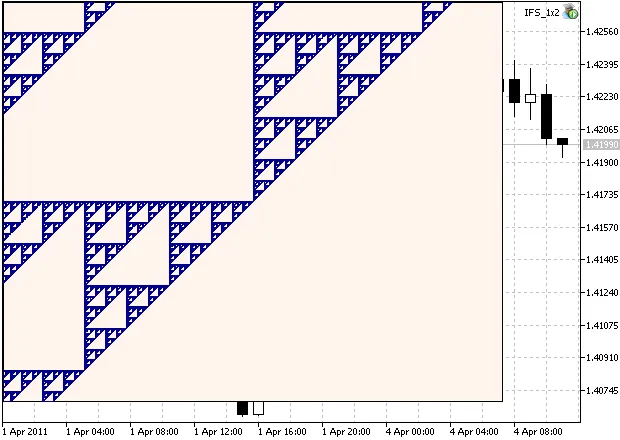
Figura 2. Regione ingrandita del Gasket di Sierpinski

Consideriamo il famoso Fern di Barnsley, proposto da Michael Barnsley. È più complesso.

Figura 3. Fern di Barnsley

Figura 3. Fern di Barnsley

Il codice è simile, ma in questo caso abbiamo 4 contrazioni IFS con pesi diversi.

//+------------------------------------------------------------------+
//|                                                     IFS_fern.mq5 |
//|                        Copyright 2011, MetaQuotes Software Corp. |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2011, MetaQuotes Software Corp."
#property link      "https://www.mql5.com"
#property version   "1.00"
#include <cIntBMP.mqh>
//-- Barnsley Fern IFS coefficients
//-- (a,b,c,d) matricies
double IFS_a[4] = {0.00,  0.85,  0.20,  -0.15};
double IFS_b[4] = {0.00,  0.04, -0.26,   0.28};
double IFS_c[4] = {0.00, -0.04,  0.23,   0.26};
double IFS_d[4] = {0.16,  0.85,  0.22,   0.24};
//-- (e,f) vectors
double IFS_e[4] = {0.00,  0.00,  0.00,   0.00};
double IFS_f[4] = {0.00,  1.60,  1.60,   0.00};
//-- "probabilities" of transforms, multiplied by 1000
double IFS_p[4] = {10,     850,    70,     70};

double Probs[4];
cIntBMP bmp;
int scale=50;
//+------------------------------------------------------------------+
//| Expert initialization function                                               |
//+------------------------------------------------------------------+
int OnInit()
  {
   double m=0;
   for(int i=0; i<ArraySize(IFS_p); i++)
     {
      Probs[i]=IFS_p[i]+m;
      m=m+IFS_p[i];
     }

   int XSize=600;
   int YSize=600;

   bmp.Create(XSize,YSize,clrSeashell);

   bmp.DrawRectangle(0,0,XSize-1,YSize-1,clrBlack);

   double x0=0;
   double y0=0;
   double x,y;

   int points=250000;

   for(int i=0; i<points; i++)
     {
      double prb=1000*(rand()/32767.0);
      for(int k=0; k<ArraySize(IFS_p); k++)
        {
         if(prb<=Probs[k])
           {
            x = IFS_a[k] * x0 + IFS_b[k] * y0 + IFS_e[k];
            y = IFS_c[k] * x0 + IFS_d[k] * y0 + IFS_f[k];
            x0 = x;
            y0 = y;
            int scX = int (MathRound(XSize/2 + (x)*scale));
            int scY = int (MathRound(YSize/2 + (y-5)*scale));
            if(scX>=0 && scX<XSize && scY>=0 && scY<YSize) { bmp.DrawDot(scX,scY,clrForestGreen); }
            break;
         }
     }
   }
   bmp.Save("bmpimg",true);
   bmp.Show(0,0,"bmpimg","IFS");
//---
   return(0);
  }
//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
   ObjectDelete(0,"IFS");
   bmp.Delete("bmpimg",true);
  }
//+------------------------------------------------------------------+

È notevole che una struttura così complessa possa essere definita da soli 28 numeri.

Se aumentiamo la scala a 150 e impostiamo le iterazioni a 1250000, vedremo il frammento ingrandito:

Figura 4. Un frammento del Fern di Barnsley

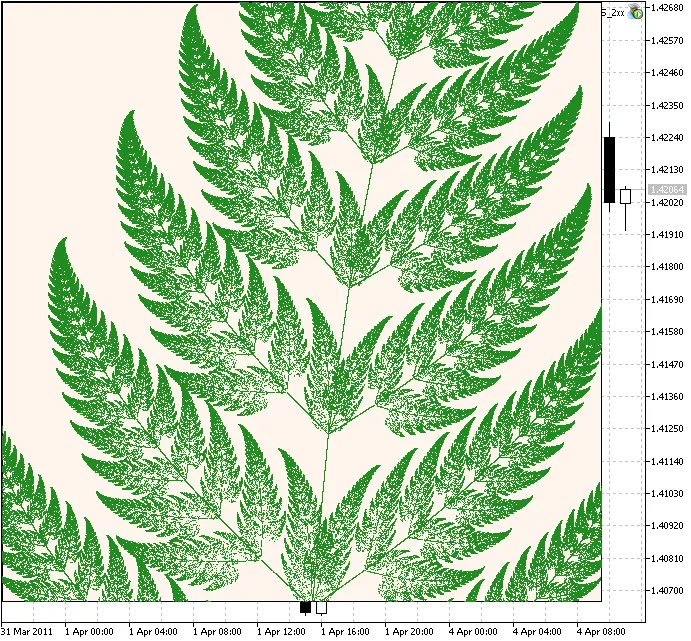
Figura 4. Un frammento del Fern di Barnsley

Come vedi, l'algoritmo è universale: consente di generare diversi insiemi frattali.

Il prossimo esempio è il Carpet di Sierpinski, definito dai seguenti coefficienti IFS:

//-- Sierpinski Gasket IFS coefficients
double IFS_a[8] = {0.333, 0.333, 0.333, 0.333, 0.333, 0.333, 0.333, 0.333};
double IFS_b[8] = {0.00,  0.00,  0.00,   0.00, 0.00,  0.00,  0.00,   0.00};
double IFS_c[8] = {0.00,  0.00,  0.00,   0.00, 0.00,  0.00,  0.00,   0.00};
double IFS_d[8] = {0.333, 0.333,  0.333,  0.333, 0.333,  0.333,  0.333, 0.333};
double IFS_e[8] = {-0.125, -3.375, -3.375,  3.125, 3.125, -3.375, -0.125, 3.125};
double IFS_f[8] = {6.75, 0.25, 6.75,  0.25, 6.75, 3.5, 0.25, 3.50};
//-- "probabilities", multiplied by 1000
double IFS_p[8]={125,125,125,125,125,125,125,125};

Figura 5. Carpet di Sierpinski

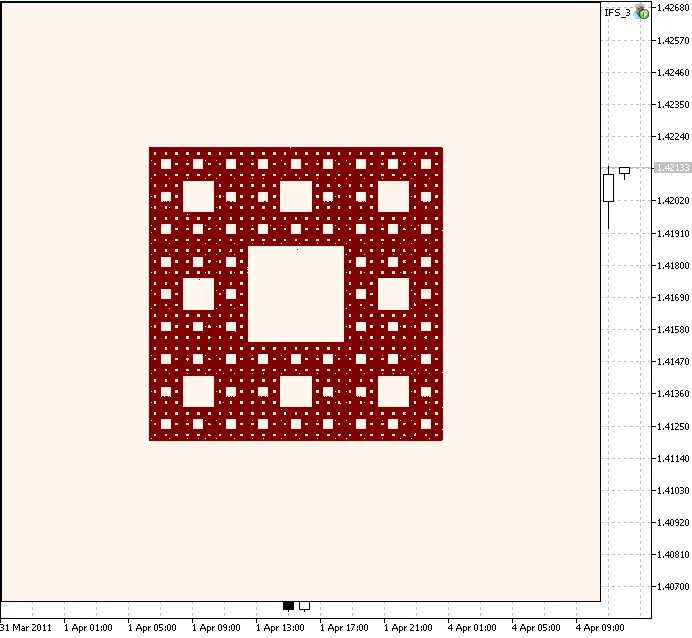
Figura 5. Carpet di Sierpinski

Nel capitolo 2, abbiamo considerato l'algoritmo di calcolo dei coefficienti delle contrazioni IFS.

Per creare le "parole frattali". In russo, la parola "Frattali" appare come:

Figura 6. La parola

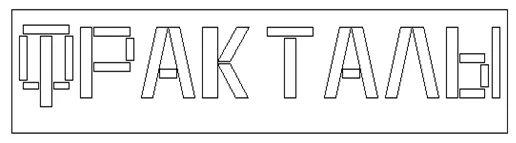
Figura 6. La parola "frattali" in russo

Per trovare i coefficienti IFS, dobbiamo risolvere i corrispondenti sistemi lineari. Le soluzioni sono:

//-- IFS coefficients of the                         
Post correlati
Elenco
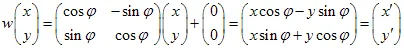
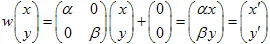
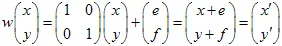
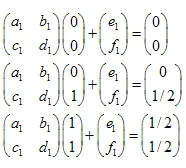
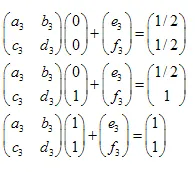
Commento (0)