저자: gpwr
버전 이력:
2009년 6월 26일 - 가격을 예측하기 전에 EMA를 사용하여 가격을 부드럽게 하는 새로운 지표 BPNN Predictor with Smoothing.mq4 추가.
2009년 8월 20일 - 산술 예외를 방지하기 위해 뉴런 활성화 함수 계산 코드를 수정; BPNN.cpp 및 BPNN.dll 업데이트
2009년 8월 21일 - DLL 실행 종료 시 메모리 정리 추가; BPNN.cpp 및 BPNN.dll 업데이트
신경망의 간단한 이론:
신경망은 입력의 함수로서 출력을 조정할 수 있는 모델입니다. 여러 개의 층으로 구성되어 있습니다:
- 입력층: 입력 데이터로 구성됨
- 은닉층: 뉴런이라고 불리는 처리 노드로 구성됨
- 출력층: 하나 이상의 뉴런으로 구성되어 있으며, 네트워크의 출력입니다.
인접한 층의 모든 노드는 서로 연결되어 있습니다. 이러한 연결을 시냅스라고 하며, 각 시냅스에는 데이터를 전파할 때 곱해지는 스케일링 계수가 할당됩니다. 이러한 스케일링 계수를 가중치(w[i][j][k])라고 합니다. 피드포워드 신경망 (FFNN)에서는 데이터가 입력에서 출력으로 전파됩니다. 아래는 하나의 입력층, 하나의 출력층 및 두 개의 은닉층이 있는 FFNN의 예입니다:
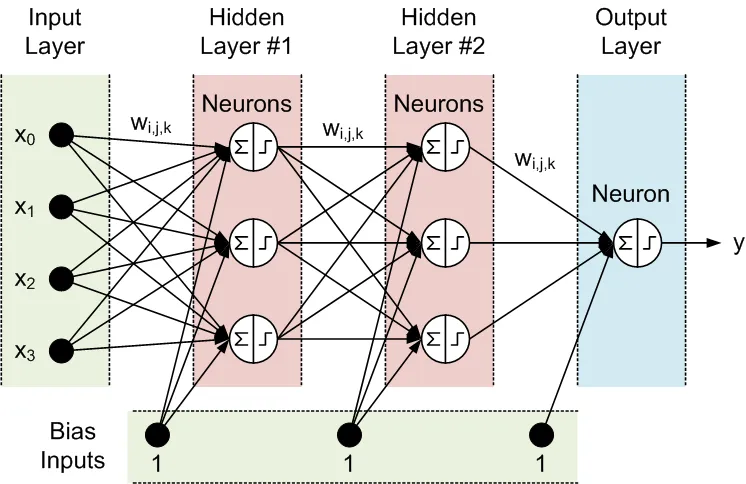
FFNN의 토폴로지는 종종 다음과 같이 약칭됩니다: <입력 수> - <첫 번째 은닉층의 뉴런 수> - <두 번째 은닉층의 뉴런 수> -...- <출력 수>. 위 네트워크는 4-3-3-1 네트워크로 언급될 수 있습니다.
데이터는 두 단계에서 뉴런에 의해 처리됩니다. 이 단계는 원의 안쪽에 나타나며, 첫 번째는 합산 기호, 두 번째는 단계 기호입니다:
- 모든 입력은 관련 가중치와 곱해진 후 합산됩니다.
- 결과 합산값은 뉴런의 활성화 함수에 의해 처리되며, 이 값이 뉴런 출력이 됩니다.
뉴런의 활성화 함수는 신경망 모델에 비선형성을 부여합니다. 활성화 함수가 없다면 은닉층을 두는 이유가 없으며, 신경망은 선형 자기회귀(AR) 모델이 됩니다.
사전 제공된 라이브러리 파일은 세 가지 활성화 함수 중에서 선택할 수 있습니다:
- 시그모이드: sigm(x)=1/(1+exp(-x)) (#0)
- 하이퍼볼릭 탄젠트: tanh(x)=(1-exp(-2x))/(1+exp(-2x)) (#1)
- 유리 함수: x/(1+|x|) (#2)
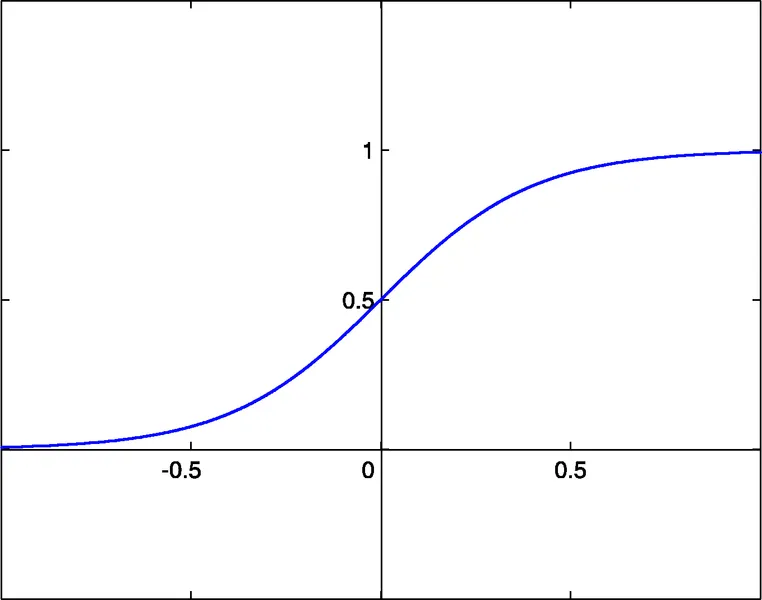
이 함수의 활성화 임계값은 x=0입니다. 이 임계값은 각 뉴런의 바이어스 입력이라는 추가 입력 덕분에 x축을 따라 이동할 수 있습니다. 바이어스 입력에도 가중치가 할당됩니다.
입력 수, 출력 수, 은닉층 수, 각 층의 뉴런 수 및 시냅스 가중치 값은 FFNN을 완벽하게 설명합니다. 즉, 생성하는 비선형 모델입니다. 가중치를 찾기 위해 네트워크는 훈련을 받아야 합니다. 지도 학습 과정 동안, 여러 세트의 과거 입력과 해당 기대 출력을 네트워크에 공급합니다. 가중치는 네트워크 출력과 기대 출력 간의 오차를 최소화하기 위해 최적화됩니다. 가중치 최적화의 가장 간단한 방법은 오차 역전파로, 이는 경량 하강법을 사용합니다. 사전 제공된 훈련 함수 Train()은 이 방법의 변형인 개선된 저항 역전파 플러스(iRProp+)를 사용합니다. 이 방법은 다음 링크에서 설명됩니다:
http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.17.1332
경량 기반 최적화 방법의 주요 단점은 종종 로컬 최소값을 찾는다는 것입니다. 가격 시계열과 같은 혼란스러운 시계열의 경우, 훈련 오류 표면은 복잡한 모양을 가지며 많은 로컬 최소값이 존재합니다. 이러한 시계열의 경우, 유전 알고리즘이 선호되는 훈련 방법입니다.
제공된 파일:
- BPNN.dll - 라이브러리 파일
- BPNN.zip - BPNN.dll을 C++로 컴파일하는 데 필요한 모든 파일의 아카이브
- BPNN Predictor.mq4 - 미래 오픈 가격을 예측하는 지표
- BPNN Predictor with Smoothing.mq4 - 부드럽게 된 오픈 가격을 예측하는 지표
파일 BPNN.cpp에는 두 개의 함수가 있습니다: Train()과 Test().
Train() 함수는 제공된 과거 입력 및 기대 출력 값을 기반으로 네트워크를 훈련시키는 데 사용됩니다. Test() 함수는 최적화된 가중치를 사용하여 네트워크 출력을 계산하는 데 사용됩니다.
여기 Train() 함수의 입력(초록) 및 출력(파랑) 매개변수 목록입니다:
double inpTrain[] - 입력 훈련 데이터 (2D 데이터를 담고 있는 1D 배열, 오래된 것이 먼저)
double outTarget[] - 훈련을 위한 출력 목표 데이터 (2D 데이터를 1D 배열로, 오래된 것이 먼저)
double outTrain[] - 훈련에서 네트워크 출력을 담고 있을 1D 배열
int ntr - 훈련 세트 수
int UEW - 초기화에 외부 가중치 사용 (1=extInitWt 사용, 0=무작위 사용)
double extInitWt[] - 외부 초기 가중치를 담고 있는 1D 배열
double trainedWt[] - 훈련된 가중치의 3D 배열을 담고 있을 1D 배열
int numLayers - 입력, 은닉 및 출력 포함 층 수
int lSz[] - 각 층의 뉴런 수. lSz[0]는 네트워크 입력 수
int AFT - 뉴런 활성화 함수 종류 (0:시그모이드, 1:하이퍼볼릭 탄젠트, 2:x/(1+x))
int OAF - 출력층 활성화 함수 활성화; 1=활성화, 0=비활성화
int nep - 최대 훈련 에폭 수
double maxMSE - 최대 MSE; maxMSE에 도달하면 훈련 중지.
여기 Test() 함수의 입력(초록) 및 출력(파랑) 매개변수 목록입니다:
double inpTest[] - 입력 테스트 데이터 (2D 데이터를 1D 배열로, 오래된 것이 먼저)
double outTest[] - 훈련 출력의 1D 배열로, 오래된 것이 먼저
int ntt - 테스트 세트 수
double extInitWt[] - 외부 초기 가중치를 담고 있는 1D 배열
int numLayers - 입력, 은닉 및 출력 포함 층 수
int lSz[] - 각 층의 뉴런 수. lSz[0]는 네트워크 입력 수
int AFT - 뉴런 활성화 함수 종류 (0:시그모이드, 1:하이퍼볼릭 탄젠트, 2:x/(1+x))
int OAF - 출력층 활성화 함수 활성화; 1=활성화, 0=비활성화
출력층에서 활성화 함수를 사용할지 여부(OAF 매개변수 값)는 출력의 성격에 따라 다릅니다. 출력이 이진인 경우, 즉 분류 문제에서 자주 발생하는 경우, 출력층에서 활성화 함수를 사용해야 합니다 (OAF=1). 활성화 함수 #0 (시그모이드)은 0과 1의 포화 수준을 가지지만, 활성화 함수 #1과 #2는 -1과 1의 수준을 가집니다. 네트워크 출력이 가격 예측인 경우, 출력층에서 활성화 함수가 필요하지 않습니다 (OAF=0).
신경망 라이브러리 사용 예시:
BPNN Predictor.mq4 - 미래 오픈 가격을 예측합니다. 네트워크의 입력은 상대 가격 변화입니다:
x[i]=Open[test_bar]/Open[test_bar+delay[i]]-1.0
여기서 delay[i]는 피보나치 수 (1, 2, 3, 5, 8, 13, 21..)로 계산됩니다. 네트워크의 출력은 다음 가격의 상대 변화 예측입니다. 출력층에서는 활성화 함수가 꺼져 있습니다 (OAF=0).
지표 입력:
extern int lastBar - 과거 데이터에서 마지막 바
extern int futBars - 예측할 미래 바 수
extern int numLayers - 입력, 은닉 및 출력 포함 층 수 (2..6)
extern int numInputs - 입력 수
extern int numNeurons1 - 첫 번째 은닉 또는 출력층의 뉴런 수
extern int numNeurons2 - 두 번째 은닉 또는 출력층의 뉴런 수
extern int numNeurons3 - 세 번째 은닉 또는 출력층의 뉴런 수
extern int numNeurons4 - 네 번째 은닉 또는 출력층의 뉴런 수
extern int numNeurons5 - 다섯 번째 은닉 또는 출력층의 뉴런 수
extern int ntr - 훈련 세트 수
extern int nep - 최대 에폭 수
extern int maxMSEpwr - 최대 MSE=10^maxMSEpwr; 훈련이 extern int AFT - 활성화 함수 종류 (0:시그모이드, 1:하이퍼볼릭 탄젠트, 2:x/(1+x))
이 지표는 차트에 세 가지 곡선을 플롯합니다:
- 빨간색 - 미래 가격 예측
- 검은색 - 과거 훈련 오픈 가격, 네트워크의 기대 출력을 위해 사용됨
- 파란색 - 훈련 입력에 대한 네트워크 출력
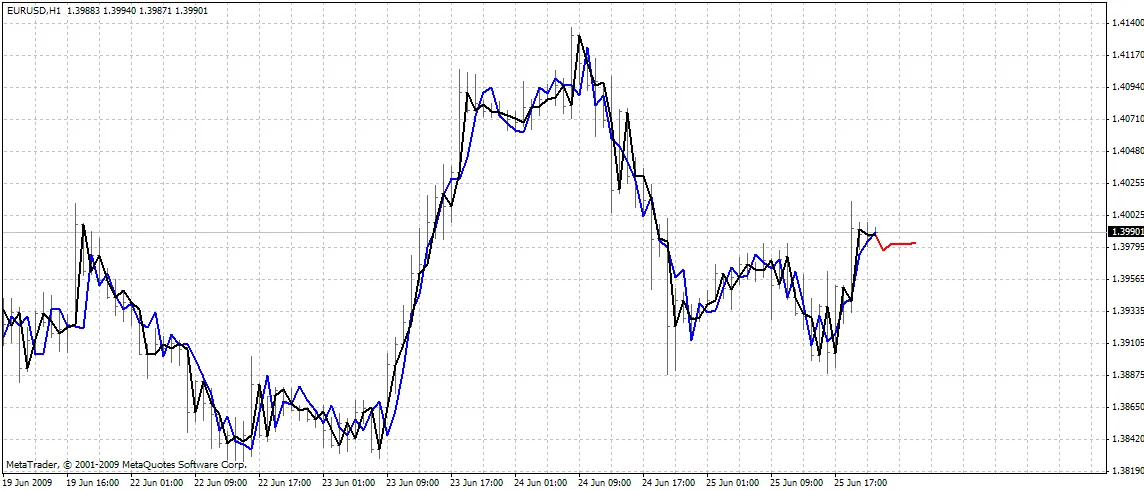
BPNN Predictor.mq4 - 미래의 부드러운 오픈 가격을 예측합니다. EMA 부드러움을 사용하여 smoothPer 기간 동안 처리됩니다.
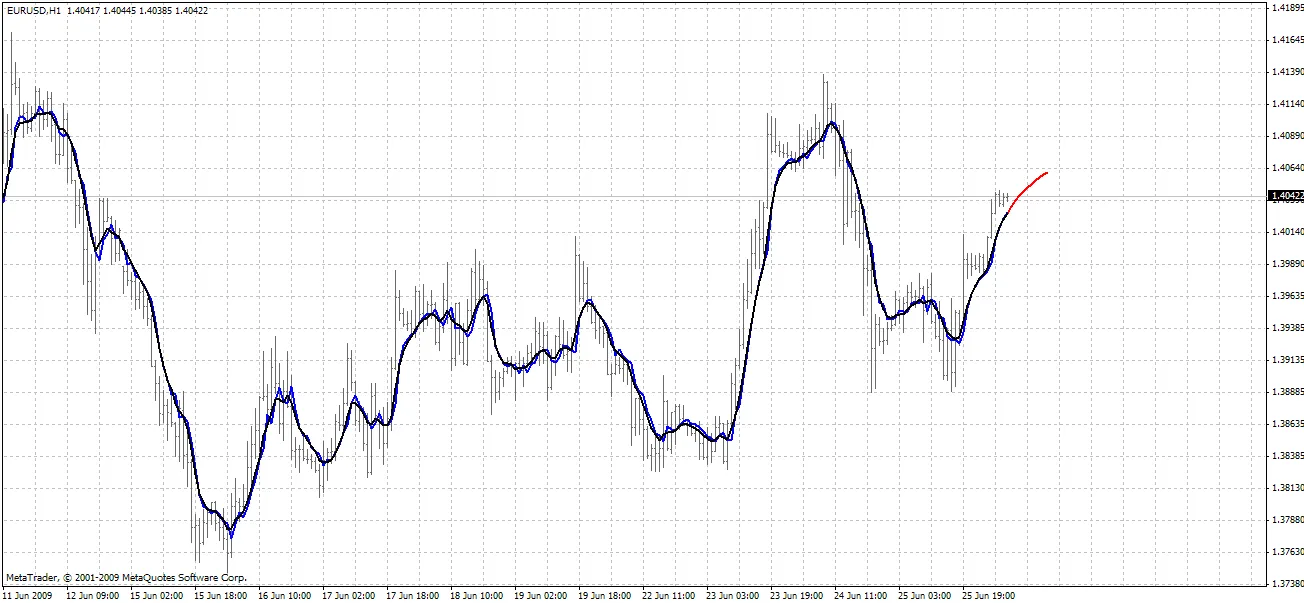
설정 방법:
- 제공된 BPNN.DLL을 C:\Program Files\MetaTrader 4\experts\libraries에 복사하세요.
- 메타트레이더에서: 도구 - 옵션 - 전문가 고문 - DLL 가져오기 허용
또한 BPNN.zip의 소스 코드를 사용하여 자신의 DLL 파일을 컴파일할 수 있습니다.
추천 사항:
- 세 개의 레이어(numLayers=3: 하나의 입력, 하나의 은닉 및 하나의 출력)로 구성된 네트워크는 대다수의 경우에 충분합니다. Cybenko 정리에 따르면 (1989), 하나의 은닉층이 있는 네트워크는 원하는 정확도로 모든 연속 다변량 함수를 근사할 수 있습니다; 두 개의 은닉층이 있는 네트워크는 모든 불연속 다변량 함수를 근사할 수 있습니다:
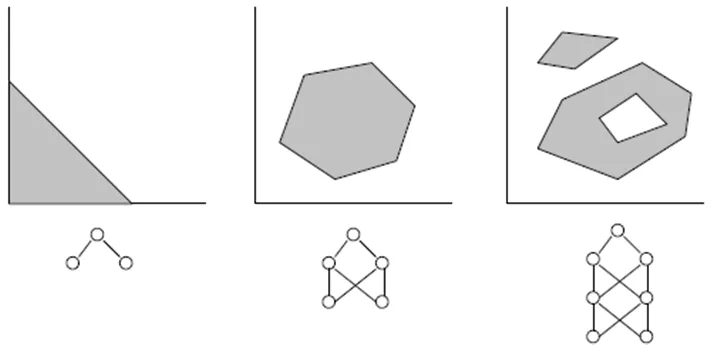
- 은닉층의 최적 뉴런 수는 시행착오를 통해 찾을 수 있습니다. 문헌에서 다음과 같은 '경험 법칙'을 찾을 수 있습니다: #의 숨겨진 뉴런 = (#의 입력 + #의 출력)/2 또는 SQRT(#의 입력 * #의 출력). 훈련 오류는 메타트레이더의 전문가 창에서 표시됩니다.
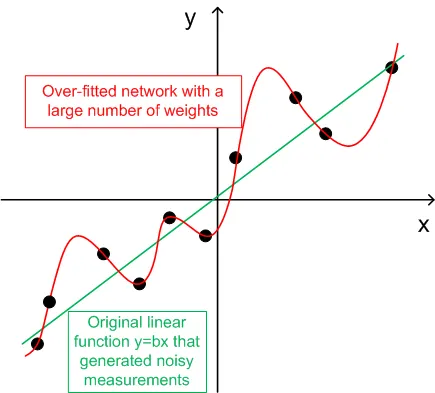
- 일반화를 위해, 훈련 세트 수(ntr)는 네트워크의 총 가중치 수의 2-5배로 선택해야 합니다. 예를 들어, 기본적으로 BPNN Predictor.mq4는 12-5-1 네트워크를 사용합니다. 총 가중치 수는 (12+1)*5+6=71입니다. 따라서 훈련 세트 수(ntr)는 최소 142 이상이어야 합니다. 일반화와 기억화 (과적합)의 개념은 아래 그래프에서 설명됩니다.
- 네트워크의 입력 데이터는 정상화되어야 합니다. 외환 가격은 정상적이지 않습니다. 입력을 -1..+1 범위로 정규화하는 것이 좋습니다.
아래 그래프는 잡음에 의해 왜곡된 선형 함수 y=b*x (x-입력, y-출력)을 보여줍니다. 이 추가된 잡음은 측정된 함수 출력 (검은 점들)을 직선에서 벗어나게 합니다. 함수 y=f(x)는 피드포워드 신경망으로 모델링할 수 있습니다. 많은 수의 가중치를 가진 네트워크는 측정된 데이터에 제로 오류로 맞출 수 있습니다. 이 동작은 모든 검은 점을 통과하는 빨간 곡선으로 보여집니다. 그러나 이 빨간 곡선은 원래의 선형 함수 y=b*x (녹색)와는 아무 관계가 없습니다. 이 과적합된 네트워크를 사용하여 함수 y(x)의 미래 값을 예측하면 추가된 잡음의 무작위성으로 인해 큰 오류가 발생합니다.
이 코드를 공유하는 대가로, 저자는 작은 부탁을 드립니다. 이 코드를 기반으로 수익성 있는 거래 시스템을 만들 수 있었다면, 저에게 직접 이메일을 보내어 아이디어를 공유해 주시기 바랍니다: vlad1004@yahoo.com.
행운을 빕니다!

댓글 0